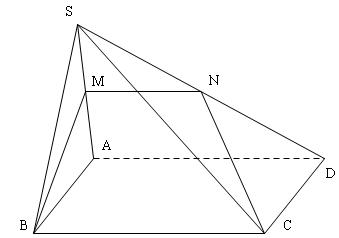
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $SA$ vuông góc với đáy. Độ dài các cạnh $AB = a; AD = b; SA = 2a$. Gọi $M$ là trung điểm của đoạn $SA.$Mặt phẳng ($MBC$) cắt hình chóp theo thiết diện gì? Tính diện tích thiết diện đó

Lời giải

Giao tuyến của mp $(MBC)$ và mp $(SAD)$ cắt $SD$ tại $N:MN//BC$ vì $AD//BC$
$MB\bot BC$ vì $BC\bot mp(SAB)$.Vậy thiết diện là hình thang vuông $MNCB$
dt$(MNCB)=\frac{MN+BC}{2} .BM$
có $MN=\frac{AD}{2} = \frac{b}{2}   $
$BM=\sqrt{AM^2+AB^2}=\sqrt{a^2+a^2}=a\sqrt{2}   $
Vậy dt$(MNCB)=\frac{\frac{b}{2}+b }{2} a \sqrt{2} = \frac{3\sqrt{2} }{4}  ab$ (đvdt)