Hình học không gian

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có cạnh bên $BB'=a$ và $BB'$ tạo với mặt phẳng $ABC$ góc $60^0$. Giả sử $ABC$ là tam giác vuông tại $C$ và $\widehat{BAC}=60^0$.Hình chiếu vuông góc của $B'$ lên $(ABC)$ trùng với trọng tâm tam giác $ABC$.Tính thể tích tứ diện $A'ABC$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

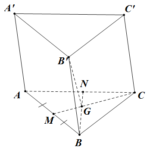
Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có cạnh bên $BB'=a$ và $BB'$ tạo với mặt phẳng $ABC$ góc $60^0$. Giả sử $ABC$ là tam giác vuông tại $C$ và $\widehat{BAC}=60^0$.Hình chiếu vuông góc của $B'$ lên $(ABC)$ trùng với trọng tâm tam giác $ABC$.Tính thể tích tứ diện $A'ABC$. Lời giải Gọi $G$ là trong tâm tam giác $ABC$ ta có … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có cạnh bên $BB'=a$ và $BB'$ tạo với mặt phẳng $ABC$ góc $60^0$. Giả sử $ABC$ là tam giác vuông tại $C$ và $\widehat{BAC}=60^0$.Hình chiếu vuông góc của $B'$ lên $(ABC)$ trùng với trọng tâm tam giác $ABC$.Tính thể tích tứ diện $A'ABC$.

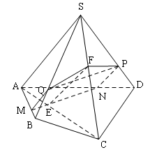
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Thể tích khối đa diện

Đề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$. Lời giải Do $MS=MA\Rightarrow d(A,(MNP))=d(S,(MNP)) (1) \Rightarrow V_{A.MNP}=V_{S.MNP}$Theo bài toán cơ bản, ta có:$\frac{V_{SMNP}}{V_{S.ABP}}=\frac{SM}{SA}.\frac{SN}{SB}=\frac{1}{4}\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$.

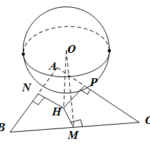
Đề bài: Cho hình cầu $(S)$ tâm $O$ bán kính $R=5cm$. Tam giác $ABC$ với ba cạnh $BC=13cm, CA=14cm, AB=15cm$, trong đó cả ba cạnh cùng tiếp xúc với mặt cầu. Tìm khoảng cách từ tâm $O$ đến mặt phẳng $(ABC)$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

Đề bài: Cho hình cầu $(S)$ tâm $O$ bán kính $R=5cm$. Tam giác $ABC$ với ba cạnh $BC=13cm, CA=14cm, AB=15cm$, trong đó cả ba cạnh cùng tiếp xúc với mặt cầu. Tìm khoảng cách từ tâm $O$ đến mặt phẳng $(ABC)$. Lời giải Giả sử $AB,BC,CA$ lần lượt tiếp xúc với mặt cầu tại $N,M,P$. Như vậy ta có:$ON \bot AB, OM \bot BC, OP \bot CA$.Kẻ $OH\bot (ABC)$. Theo định lí ba đường … [Đọc thêm...] vềĐề bài: Cho hình cầu $(S)$ tâm $O$ bán kính $R=5cm$. Tam giác $ABC$ với ba cạnh $BC=13cm, CA=14cm, AB=15cm$, trong đó cả ba cạnh cùng tiếp xúc với mặt cầu. Tìm khoảng cách từ tâm $O$ đến mặt phẳng $(ABC)$.

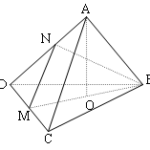
Đề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$ Lời giải $a.$ Ta có ngay kết luận $AO\bot CD$ vì $A.BCD$ là hình chóp tam giác đều$b.$ Gọi $N$ là trung điểm $AD$ ta có: $MN//AC\Rightarrow (AC,BM)=\widehat{BMN} $Xét $\Delta BMN$ … [Đọc thêm...] vềĐề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$

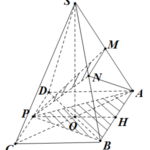
Đề bài: Cho hình chóp $S.ABCD$.Trên đoạn thẳng $AC$ lấy một điểm $E$ và trên cạnh $SC$ lấy mọt điểm $F$ sao cho :$\frac{AE}{AC} =\frac{SF}{SC} $Một mặt phẳng $(\alpha )$ đi qua đường thẳng $EF$ cắt các đường thẳng $AB,AD,SD,SB$ theo thứ tự tại các điểm $M,N,P,Q$$a.$ Chứng minh $MQ//NP$$b.$ Xác định vị trí các điểm $M,N$ để tứ giác $MNPQ$ là hình bình hành và thiết diện của hình chóp trong trường hợp này

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he song song

Đề bài: Cho hình chóp $S.ABCD$.Trên đoạn thẳng $AC$ lấy một điểm $E$ và trên cạnh $SC$ lấy mọt điểm $F$ sao cho :$\frac{AE}{AC} =\frac{SF}{SC} $Một mặt phẳng $(\alpha )$ đi qua đường thẳng $EF$ cắt các đường thẳng $AB,AD,SD,SB$ theo thứ tự tại các điểm $M,N,P,Q$$a.$ Chứng minh $MQ//NP$$b.$ Xác định vị trí các điểm $M,N$ để tứ giác $MNPQ$ là hình bình hành và thiết diện của hình … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$.Trên đoạn thẳng $AC$ lấy một điểm $E$ và trên cạnh $SC$ lấy mọt điểm $F$ sao cho :$\frac{AE}{AC} =\frac{SF}{SC} $Một mặt phẳng $(\alpha )$ đi qua đường thẳng $EF$ cắt các đường thẳng $AB,AD,SD,SB$ theo thứ tự tại các điểm $M,N,P,Q$$a.$ Chứng minh $MQ//NP$$b.$ Xác định vị trí các điểm $M,N$ để tứ giác $MNPQ$ là hình bình hành và thiết diện của hình chóp trong trường hợp này

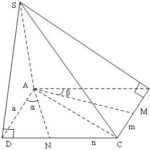
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Đoạn $SA$ cố định vuông góc với $(P)$ tại $A$. $M,N$ lần lượt là các điểm di động trên cạnh $BC$ và $CD$. Đặt $BM=u, DN=v$. Chứng minh rằng $a(u+v)+uv=a^2$ là điều kiện cần và đủ để hai mặt phẳng $(SAM),(SAN)$ tạo với nhau một góc $45^0$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Đoạn $SA$ cố định vuông góc với $(P)$ tại $A$. $M,N$ lần lượt là các điểm di động trên cạnh $BC$ và $CD$. Đặt $BM=u, DN=v$. Chứng minh rằng $a(u+v)+uv=a^2$ là điều kiện cần và đủ để hai mặt phẳng $(SAM),(SAN)$ tạo với nhau một góc $45^0$. Lời giải ta có: $(SAM) \cap (SAN)=SA$Vì $SA\bot … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Đoạn $SA$ cố định vuông góc với $(P)$ tại $A$. $M,N$ lần lượt là các điểm di động trên cạnh $BC$ và $CD$. Đặt $BM=u, DN=v$. Chứng minh rằng $a(u+v)+uv=a^2$ là điều kiện cần và đủ để hai mặt phẳng $(SAM),(SAN)$ tạo với nhau một góc $45^0$.

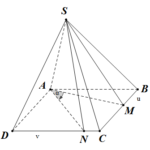
Đề bài: Trong mặt phẳng ($P$) cho hình vuông $ABCD$ có cạnh bằng $a, S$ là một điểm bất kì nằm trên đường thẳng $At $ vuông góc với mặt phẳng $(P$) tại $A$.$1.$ Tính theo $a$ thể tích hình cầu ngoại tiếp hình chóp $S.ABCD$ khi $SA = 2a$.$2$. $M, N$ lần lượt là hai điểm di động trên các cạnh $CB, CD (M \in CB ;\,\,N \in CD)$ và đặt $CM = m, CN = n$. Tìm một biểu thức liên hệ giữa $m$ và $n$ để các mặt phẳng $(SMA)$ và $(SAN)$ tạo với nhau một góc ${45^0}$

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Trong mặt phẳng ($P$) cho hình vuông $ABCD$ có cạnh bằng $a, S$ là một điểm bất kì nằm trên đường thẳng $At $ vuông góc với mặt phẳng $(P$) tại $A$.$1.$ Tính theo $a$ thể tích hình cầu ngoại tiếp hình chóp $S.ABCD$ khi $SA = 2a$.$2$. $M, N$ lần lượt là hai điểm di động trên các cạnh $CB, CD (M \in CB ;\,\,N \in CD)$ và đặt $CM = m, CN = n$. Tìm một biểu thức liên hệ … [Đọc thêm...] vềĐề bài: Trong mặt phẳng ($P$) cho hình vuông $ABCD$ có cạnh bằng $a, S$ là một điểm bất kì nằm trên đường thẳng $At $ vuông góc với mặt phẳng $(P$) tại $A$.$1.$ Tính theo $a$ thể tích hình cầu ngoại tiếp hình chóp $S.ABCD$ khi $SA = 2a$.$2$. $M, N$ lần lượt là hai điểm di động trên các cạnh $CB, CD (M \in CB ;\,\,N \in CD)$ và đặt $CM = m, CN = n$. Tìm một biểu thức liên hệ giữa $m$ và $n$ để các mặt phẳng $(SMA)$ và $(SAN)$ tạo với nhau một góc ${45^0}$

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Thể tích khối đa diện

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$ Lời giải Cần giải chi tiết ( đáp số $\frac{2}{3}\frac{a^3}{\sqrt{a^2-16h^2}}$) … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và $SH$ là đường cao của hình chóp. Khoảng cách từ trung điểm $I$ của $SH$ đến mặt bên $(SDC)$ bằng $h$. Tìm thể tích khối chóp $S.ABCD$

Đề bài: Cho tứ diện $ABCD$ có $4$ chiều cao kẻ từ $4$ đỉnh $h_1,h_2,h_3,h_4$. Gọi $r$ là bán kính hình cầu nội tiếp tứ diện. Chứng minh : $\frac{1}{h_1}+\frac{1}{h_2}+\frac{1}{h_3}+\frac{1}{h_4}=\frac{1}{r}$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

Đề bài: Cho tứ diện $ABCD$ có $4$ chiều cao kẻ từ $4$ đỉnh $h_1,h_2,h_3,h_4$. Gọi $r$ là bán kính hình cầu nội tiếp tứ diện. Chứng minh : $\frac{1}{h_1}+\frac{1}{h_2}+\frac{1}{h_3}+\frac{1}{h_4}=\frac{1}{r}$. Lời giải Cần giải chi tiết. … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$ có $4$ chiều cao kẻ từ $4$ đỉnh $h_1,h_2,h_3,h_4$. Gọi $r$ là bán kính hình cầu nội tiếp tứ diện. Chứng minh : $\frac{1}{h_1}+\frac{1}{h_2}+\frac{1}{h_3}+\frac{1}{h_4}=\frac{1}{r}$.

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$.

Ngày 25/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$. Lời giải Goi $P$ là trung điểm của $AB$ khi đó $MP//EB (1)$Ta có: $SE// DA; SE=DA\Rightarrow SE//BC; SE=BC$$\Rightarrow SEBC $là hình binh hành … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$, cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ tương ứng là trung điểm của $AE, BC$. Tìm khoảng cách theo $a$ giữa hai đường thẳng $MN,AC$.