Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có cạnh bên $BB'=a$ và $BB'$ tạo với mặt phẳng $ABC$ góc $60^0$. Giả sử $ABC$ là tam giác vuông tại $C$ và $\widehat{BAC}=60^0$.Hình chiếu vuông góc của $B'$ lên $(ABC)$ trùng với trọng tâm tam giác $ABC$.Tính thể tích tứ diện $A'ABC$.

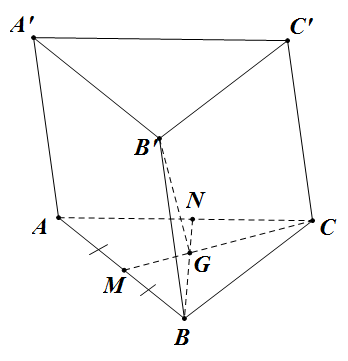
Lời giải

Gọi $G$ là trong tâm tam giác $ABC$ ta có $B’G \bot (ABC)$.Từ
đó $\widehat{B’BCG}=60^0$ là góc mà $BB’$ tạo với mặt phẳng $(ABC)$. Trong tam
giác vuông $BB’G$ ta có ngay: $BG=\frac{a}{2}, B’G=\frac{a\sqrt {3}}{2}$

 Đặt $AB=2x$, trong tam giác vuông $ABC$ ta có:
  $AC=x, BC=x\sqrt{3} $ (do $\widehat{ABC}=60^0$)
Giả sử $BG \cap AC$ thì $BN=\frac{a}{2}BG=\frac{3a}{4}$.
Áp dụng định lí py ta go trong tam giác vuông $BNC$ ta có:
  $BN^2=NC^2+BC^2\Rightarrow \frac{9a^2}{16}=\frac{x^2}{4}+3x^2\Rightarrow
x^2=\frac{9a^2}{52}         (1)$
ta có
$V_{A’ABC}=\frac{1}{3}S_{ABC}.B’G=\frac{1}{3}.\frac{1}{2}.AB.BC.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{12}x.x\sqrt{3}=\frac{ax^2}{4}       
(2)$
thay $(2)$ vào $(1)$ ta có: $V_{A’.ABC}=\frac{9a^3}{208}$   
(đvtt).