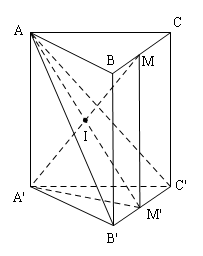
Đề bài: Cho hình lăng trụ tam giác $ABC.A'B'C'$. Gọi $M$ và $M'$ lần lượt là trung điểm của các cạnh $BC$ và $B'C'$. Tìm giao điểm của mp$(AB'C')$ với đường thẳng $A'M$

Lời giải

 Trước tiên, để ý rằng $AMM’A’$ là hình bình hành.
Thật vậy, ta có $MM\parallel BB’$ và $MM’=BB’$. Mặt khác:
$AA’\parallel BB’$ và $AA’=BB’$
nên từ đó, $MM’\parallel AA’$ và $MM’=AA’$. Suy ra $AA’M’M$ là hình bình hành. Vậy $AM’$ và $A’M$ giao nhau tại trung điểm $I$ của mỗi đường.
Bây giờ, dễ thấy $AM’$ nằm trong mặt phẳng $(AB’C’)$, nên $I$ chính là giao điẻm của đường thẳng $A’M$ với mp$(AB’C’)$.