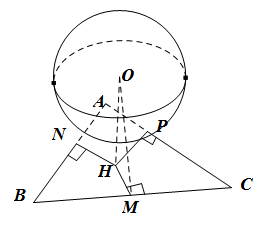
Đề bài: Cho hình cầu $(S)$ tâm $O$ bán kính $R=5cm$. Tam giác $ABC$ với ba cạnh $BC=13cm, CA=14cm, AB=15cm$, trong đó cả ba cạnh cùng tiếp xúc với mặt cầu. Tìm khoảng cách từ tâm $O$ đến mặt phẳng $(ABC)$.

Lời giải

Giả sử $AB,BC,CA$ lần lượt tiếp xúc với mặt cầu tại $N,M,P$. Như vậy ta có:
$ON \bot AB, OM \bot BC, OP \bot CA$.
Kẻ $OH\bot (ABC)$. Theo định lí ba đường vuông góc ta có: $HM\bot BC, HN\bot AB, HP\bot CA$.
Vì $ON=OM=OP=R\Rightarrow HM=HN=HP$.
Vậy $H$ là trọng tâm đường tròn nội tiếp tam giác $ABC$ với bán kinh $r=HM$.

Áp dụng công thức $r=\frac{S}{p}$, ở đây $S,p$ tương ứng là diện tích và nửa chu vi của tam giác $ABC$ ta có: $p=\frac{13+14+15}{2}=21$.
Theo công thức Hê-rông ta có: $S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{21.8.7.6}=84$
Từ đó suy ra $r=4cm$. Do vậy theo định lí Pytago thì khoảng cách từ $O$ đến $(ABC)$ là :
$OH=\sqrt{5^2-4^2}=3cm$.