Đề bài: Một hình trụ nội tiếp một hình cầu, có tỉ số giữa diện tích toàn phần của hình trụ và diện tích hình cầu bằng $m$. Xác định tỉ số giữa bán kính đáy của hình trụ và bán kính hình cầu để $m$ lớn nhất.

Lời giải

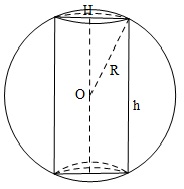
Giả sử bán kính hình cầu bằng $R$, bán kính hình trụ bằng $r$, đường cao hình trụ bằng $h$.
Ta có: $h=2OH=2\sqrt{R^2-r^2}=2R\sqrt{1-\frac{r^2}{R^2}}$
Ta có, theo giả thiết: $\frac{2\pi r^2+2\pi r.2\sqrt{R^2-r^2}}{4\pi R^2}=m$
           $\Leftrightarrow \frac{r^2}{2R^2}+\frac{r}{R}\sqrt{(1-\frac{r^2}{R^2})}=m>0$
Đặt $\frac{r^2}{R^2}=k$, ta có: $k+2\sqrt{(k(1-k)}=2m \Leftrightarrow 5k^2-4(m+1)+4m^2=0   (1)$
$\Delta’=4(m+1)^2-20m^2=4(1+2m-4m^2)$ và $(1)$ có nghiệm khi:
$1+2m-4m^2\geq 0 \Rightarrow 0Vậy $m$ lớn nhất bằng $\frac{1+\sqrt{5}}{4}$ khi $k=\frac{2(m+1)}{5}=\frac{5+\sqrt{5}}{10}$