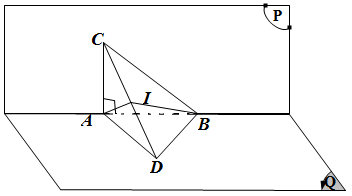
Đề bài: Cho hai mặt phẳng $(P), (Q)$ vuông góc với nhau có giao tuyến là $\Delta$. Trên $\Delta$ lấy hai điểm $A,B$ sao cho $AB=a$. Trong mặt phẳng $(P)$ lấy điểm $C$, trong $(Q)$ lấy điểm $D$ sao cho $AC,BD$ cùng vuông góc với $\Delta$. Giả sử $AC=BD=AB$. Chứng minh rằng bốn điểm $A,B,C,D$ nằm trên một mặt cầu và tìm bán kính của hình cầu ấy.

Lời giải

Do $(P)\bot (Q); (P)\cap (Q)=\Delta$,
mà $AC\bot \Delta\Rightarrow AC\bot (Q)\Rightarrow AC\bot AD$.
Tương tự ta có $DB\bot BC$.

Vì thế gọi $I$ là trung điểm của $CD$, thì trong các tam giác vuông $CAD,CBD$ ta có:
$IC=ID=IA; IC=ID=IB$.
Suy ra $IA=IB=IC=ID$, tức là bốn điểm $A,B,C,D$ cùng nằm trên một mặt cầu tâm $I$ bán kính $R=\frac{1}{2}CD  (1)$
Ta có: $CD^2=CA^2+AD^2=CA^2+BA^2+BD^2=3a^2  (2)$.
Từ $(1), (2)$ suy ra $R=\frac{a\sqrt{3}}{2}$