Đề bài: Tính thể tích khôi tứ diện $ABCD$ biết $AB=a, AC=b,AD=c$ và các góc $\widehat{ABC},\widehat{CAD},\widehat{DAB}$ đều bằng $60^0$. Lời giải cần giải chi tiết (đáp số $\frac{abc\sqrt{2}}{12})$. … [Đọc thêm...] vềĐề bài: Tính thể tích khôi tứ diện $ABCD$ biết $AB=a, AC=b,AD=c$ và các góc $\widehat{ABC},\widehat{CAD},\widehat{DAB}$ đều bằng $60^0$.
Hình học không gian
Đề bài: Tứ diện $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $H$ và $K$ lần lượt là trọng tâm của các tam giác $ABC$ và $SBC$.1. Chứng minh $SC$ vuông góc với mặt phẳng $(BHK)$ và $(SAC)\bot (BHK)$.2. Chứng minh $HK \bot (SBC)$ và $(SBC)\bot (BHK)$.
Đề bài: Tứ diện $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $H$ và $K$ lần lượt là trọng tâm của các tam giác $ABC$ và $SBC$.1. Chứng minh $SC$ vuông góc với mặt phẳng $(BHK)$ và $(SAC)\bot (BHK)$.2. Chứng minh $HK \bot (SBC)$ và $(SBC)\bot (BHK)$. Lời giải cần giải chi tiết. … [Đọc thêm...] vềĐề bài: Tứ diện $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$. Gọi $H$ và $K$ lần lượt là trọng tâm của các tam giác $ABC$ và $SBC$.1. Chứng minh $SC$ vuông góc với mặt phẳng $(BHK)$ và $(SAC)\bot (BHK)$.2. Chứng minh $HK \bot (SBC)$ và $(SBC)\bot (BHK)$.
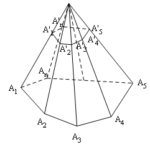
Đề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy.
Đề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy. Lời giải Giả sử hình chóp đã cho là $S.A_1A_2...A_n$; mp$(P)$ song song với mặt phẳng đáy của hình chóp cắt cạnh bên $SA_1,...SA_n$ lần lượt tại … [Đọc thêm...] vềĐề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy.
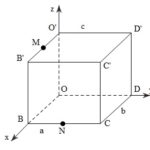
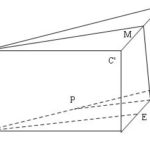
Đề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$
Đề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$ Lời giải a) Viết phương trình mặt phẳng $(\alpha )$ qua $M$ và song … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $OBCD.O'B'C'D'$ có $OB=a, OD=b, OO'=c$. $M$ và $N$ lần lượt là trung điểm các cạnh $OB'$ và $BC$a) viết phương trình mặt phẳng đi qua $M$ và song song với hai đường thẳng $O'N$ và $B'D$b) Tính thể tích hình khối chóp $O'OND$
Đề bài: Cho $ABCD$ là tứ diện có các cặp cạnh đối vuông góc với nhau. Chứng minh rằng trung điểm của các cạnh và các đường vuông góc chung của các cặp cạnh đối diện nằm trên một mặt cầu.
Đề bài: Cho $ABCD$ là tứ diện có các cặp cạnh đối vuông góc với nhau. Chứng minh rằng trung điểm của các cạnh và các đường vuông góc chung của các cặp cạnh đối diện nằm trên một mặt cầu. Lời giải Cần giải chi tiết. … [Đọc thêm...] vềĐề bài: Cho $ABCD$ là tứ diện có các cặp cạnh đối vuông góc với nhau. Chứng minh rằng trung điểm của các cạnh và các đường vuông góc chung của các cặp cạnh đối diện nằm trên một mặt cầu.
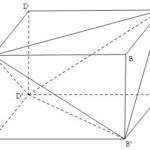
Đề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$
Đề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$ Lời giải Hình hộp chữ nhật có thể tích: $\begin{array}{l}V = abc\\{V_{{\rm{AA}}'B'D'}} = \frac{1}{6}abc\,\,\,;\,{V_{CC'D'B}} = \frac{1}{6}abc;\\{V_{BB'AC}} = \frac{1}{6}abc\,\,;\,\,{V_{{\rm{DD}}'AC}} = \frac{1}{6}abc\\ \Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $AA’ = a, AB = b, AC = c$. Tính thể tích của tứ diện $ACB’D’$ theo $a, b, c$
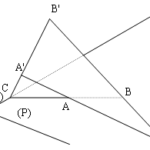
Đề bài: Cho hai mặt phẳng $(P), (Q)$ cắt nhau theo giao tuyến $d$. Cho $A, B$ là hai điểm thuộc $d$. Gọi $O$ là điểm tùy ý nằm ngoài $(P), (Q)$. Giả sử các đường thẳng $OA, OB$ lần lượt cắt $(Q)$ tại $A'$ và đường thẳng $AB$ cắt $d$ tại $C$.a) Ba điểm $O, A, B$ có thể thẳng hàng không, tại sao?b) Chứng minh ba đường thẳng $AB, A'B'$ và $d$ đồng quy.
Đề bài: Cho hai mặt phẳng $(P), (Q)$ cắt nhau theo giao tuyến $d$. Cho $A, B$ là hai điểm thuộc $d$. Gọi $O$ là điểm tùy ý nằm ngoài $(P), (Q)$. Giả sử các đường thẳng $OA, OB$ lần lượt cắt $(Q)$ tại $A'$ và đường thẳng $AB$ cắt $d$ tại $C$.a) Ba điểm $O, A, B$ có thể thẳng hàng không, tại sao?b) Chứng minh ba đường thẳng $AB, A'B'$ và $d$ đồng quy. Lời … [Đọc thêm...] vềĐề bài: Cho hai mặt phẳng $(P), (Q)$ cắt nhau theo giao tuyến $d$. Cho $A, B$ là hai điểm thuộc $d$. Gọi $O$ là điểm tùy ý nằm ngoài $(P), (Q)$. Giả sử các đường thẳng $OA, OB$ lần lượt cắt $(Q)$ tại $A'$ và đường thẳng $AB$ cắt $d$ tại $C$.a) Ba điểm $O, A, B$ có thể thẳng hàng không, tại sao?b) Chứng minh ba đường thẳng $AB, A'B'$ và $d$ đồng quy.
Đề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên
Đề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên Lời giải $1.$ Gọi $M, P, E$ là trung điểm $A’C ', AB,AC$. Gọi $N$ là trung điểm $AE$. Ta sẽ chứng tỏ $M’MNP$ là thiết diện … [Đọc thêm...] vềĐề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên
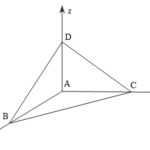
Đề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$
Đề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$ Lời giải $\Delta ABC$ vuông tại $A$ vì $BC^2=25=AB^2+AC^2$Gắn hệ trục tọa độ như hình vẽ thì $A(0;0;0),, B(3;0;0), C(0;4;0), D(0;0;4)$Phương trình mặt chắn $(BCD):\frac{x}{3}+\frac{y}{4}+\frac{z}{4}=1\Leftrightarrow 4x+3y+3z-12=0 $Vậy: … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$ có $AD\bot mp(ABC), AC=AD=4cm, AB=3cm, BC=5cm$. Tính khoảng cách từ $A$ đến $mp(BCD)$
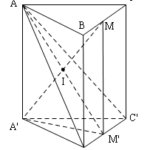
Đề bài: Cho hình lăng trụ tam giác $ABC.A'B'C'$. Gọi $M$ và $M'$ lần lượt là trung điểm của các cạnh $BC$ và $B'C'$. Tìm giao điểm của mp$(AB'C')$ với đường thẳng $A'M$
Đề bài: Cho hình lăng trụ tam giác $ABC.A'B'C'$. Gọi $M$ và $M'$ lần lượt là trung điểm của các cạnh $BC$ và $B'C'$. Tìm giao điểm của mp$(AB'C')$ với đường thẳng $A'M$ Lời giải Trước tiên, để ý rằng $AMM'A'$ là hình bình hành.Thật vậy, ta có $MM\parallel BB'$ và $MM'=BB'$. Mặt khác:$AA'\parallel BB'$ và $AA'=BB'$nên từ … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ tam giác $ABC.A'B'C'$. Gọi $M$ và $M'$ lần lượt là trung điểm của các cạnh $BC$ và $B'C'$. Tìm giao điểm của mp$(AB'C')$ với đường thẳng $A'M$