Đề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên

Lời giải

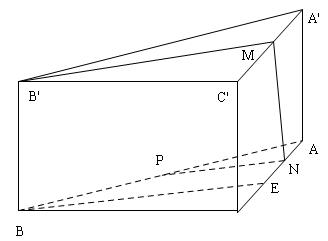
$1.$ Gọi $M, P, E$ là trung điểm $A’C ‘, AB,AC$. Gọi $N$ là trung điểm $AE$. Ta sẽ chứng tỏ $M’MNP$ là thiết diện cần tìm. Thật vậy : $B’M$ là đường cao tam giác $B’A’C’$ đều suy ra $B’M \bot A’C’\,\,\,;\,\,\,{\rm{AA}}'{\rm{AA}}(A’C’B’) \Rightarrow {\rm{AA}}’ \bot B’M$
$ \Rightarrow B’M \bot (A’AC’) \Rightarrow B’M \bot A’C \Rightarrow B’M$là một cạnh của thiết diện cần tìm.
Mặt khác do hình chữ nhật $C’A’AC$ có các kích thước $A’C’ = 2a, A’A = a$ và do $N$ là trung điểm $EA$ $ \Rightarrow \Delta EMN \sim \Delta MA’O \sim \Delta C’A’C$$ \Rightarrow MN \bot A’C
\Rightarrow $$MN$ là một cạnh nữa của thiết diện.
Lại có $NP // BE, BE \bot A’C’ \Rightarrow PN \bot A’C \Rightarrow $$PN$ là cạnh thứ ba của thiết diện $ \Rightarrow B’P$ là cạnh còn lại của thiết diện.
$2.$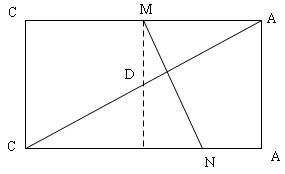

Vì $(A’B’C’) // (ABC)$ $ \Rightarrow PN//B’M \Rightarrow $Thiết diện là hình thang.Vì $BE \bot
({\rm{AA’C), PN}} \bot {\rm{(AA}}’C) \Rightarrow$ PN$ \bot MN \Rightarrow $ Thiết diện là hình
thang vuông. Thiết diện có diện tích :
$S = \frac{1}{2}\left( {PN + B’M} \right)MN = \frac{1}{2}\left( {\frac{{BE}}{2} + BE}
\right)MN = \frac{3}{4}BE.MN$
với $BE$ là (đường cao tam giác đều cạnh $2a$ )
$\begin{array}{l} \Rightarrow BE = 2a\frac{{\sqrt 3 }}{2}\\
MN = \sqrt {ME2 + EN2}  = \sqrt {a2 + \frac{{a2}}{4}} \\
 \Rightarrow S = \frac{3}{4}a\sqrt 3 \frac{{a\sqrt 5 }}{2} = \frac{{3{a^2}\sqrt {15} }}{8}
\end{array}$