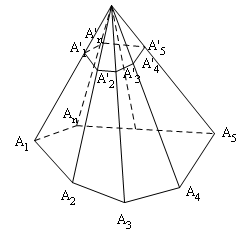
Đề bài: Gọi $(P)$ là một mặt phẳng song song với mặt đáy và không qua đỉnh của một hình chóp, cắt hình chóp  theo một thiết diện. Chứng minh rằng thiết diện tạo thành là một đa giác đồng dạng với đa giác đáy.

Lời giải

 Giả sử hình chóp đã cho là $S.A_1A_2…A_n$; mp$(P)$ song song với mặt phẳng đáy của hình chóp cắt cạnh bên $SA_1,…SA_n$ lần lượt tại $A’_1,…,A’_n$. Vì $A_1A_2$ và $A’_1A’_2$ là giao tuyến của hai mặt phẳng song song với mp$(SA_1A_2)$ nên $A_1A_2\parallel A’_1A’_2.$
Ta có: $\frac{A’_1A’_2}{A_1A_2}=\frac{SA’_2}{SA_2} .$
Tương tự ta cũng có:
$A’_2A’_3\parallel A_2A_3$ và $\frac{SA’_2}{SA_2}=\frac{A’_2A’_3}{A_2A_3}…  $
Như vậy hai đa giác $A’_1A’_2…A’_n$ và $A_1A_2…A_n$ có các cạnh tương ứng song song và tỉ số các cặp cạnh tương ứng bằng nhau (và cũng bằng $\frac{SA’_1}{SA_1}$) nên chúng đồng dạng.