Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Hình học không gian

Đề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không?

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không? Lời giải … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật đáy là hình vuông cạnh đáy bằng $2r$, chiều cao là $3,5r$. Hỏi có thể xếp vào đó 13 quả cầu bán kính $r$ hay không?

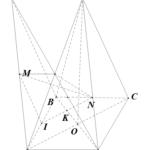
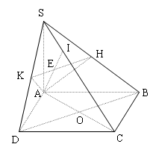
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$. Lời giải a. Gọi O là tâm của ABCDI là trung điểm của ABIN giao BO tại K$\begin{cases}IN//AC \\ BD\bot … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

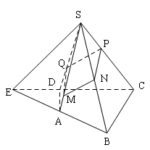
Đề bài: Cho hình chóp tứ giác $S.ABCD$.Gọi $E$ là giao điểm của hai đường thẳng $AB,CD$. Một mặt phẳng song song với đường thẳng $SE$ cắt các cạnh $SA,SB,SC$ theo thứ tự tại các điểm $M,N,P,Q$. Chứng minh $PQ//MN$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp tứ giác $S.ABCD$.Gọi $E$ là giao điểm của hai đường thẳng $AB,CD$. Một mặt phẳng song song với đường thẳng $SE$ cắt các cạnh $SA,SB,SC$ theo thứ tự tại các điểm $M,N,P,Q$. Chứng minh $PQ//MN$ Lời giải Ta có : $SE//mp (\alpha )$$SE\subset  (SAC)$$(\alpha )\cap (SAC)=PQ$$\Rightarrow  PQ//SE     (1)$Tương tự ta có $MN//SE           (2)$Từ … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$.Gọi $E$ là giao điểm của hai đường thẳng $AB,CD$. Một mặt phẳng song song với đường thẳng $SE$ cắt các cạnh $SA,SB,SC$ theo thứ tự tại các điểm $M,N,P,Q$. Chứng minh $PQ//MN$

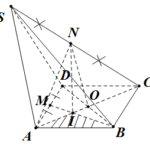
Đề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$. Lời giải Gọi $O$ là tâm của đáy $ABCD$. Trong tam giác $SAC$, ta có $NO$ là đường trung bình nên $NO // SA$, tức … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $M,N$ lần lượt là trung điểm của $AD, SC$. Giả sử $I$ là giao điểm của $BM$ và $AC$. Tính thể tích tứ diện $ANIB$.

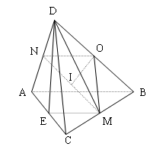
Đề bài: Cho tứ diện $ABCD.$Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,AD$$a.$ Hãy tính cosin của góc giữa $AB,DM$ biết $ABCD$ là tứ diện đều có cạnh bằng $a$$b.$ Hãy tính góc giữa $AB,CD$ biết $AB=CD=2a$ và $MN=a\sqrt{3} $

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho tứ diện $ABCD.$Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,AD$$a.$ Hãy tính cosin của góc giữa $AB,DM$ biết $ABCD$ là tứ diện đều có cạnh bằng $a$$b.$ Hãy tính góc giữa $AB,CD$ biết $AB=CD=2a$ và $MN=a\sqrt{3} $ Lời giải $a.$ Gọi $E$ là trung điểm của $AC$ ta có :$EM//AB$ và $EM=\frac{a}{2} $do đó $(AB,DM)=(MD,ME)$Xét $\Delta DEM$ ta có … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD.$Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,AD$$a.$ Hãy tính cosin của góc giữa $AB,DM$ biết $ABCD$ là tứ diện đều có cạnh bằng $a$$b.$ Hãy tính góc giữa $AB,CD$ biết $AB=CD=2a$ và $MN=a\sqrt{3} $

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA$ vuông góc với mặt phẳng $(ABCD)$.Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên $SB,SC,SD$$a.$ Chứng minh rằng $BC\bot (SAB),CD\bot (SAD)$$b.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $BD$$c.$ Chứng minh rằng $AH,AK$ cùng vuông góc với $SC$. Từ đó suy ra ba đường thẳng $AH,AI,AK$ cùng chứa trong một mặt phẳng.$d.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $HK$. Từ đó suy ra $HK\bot AI$$e.$ Tính diện tích tứ giác $AHIK$ biết $SA=AB=a$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA$ vuông góc với mặt phẳng $(ABCD)$.Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên $SB,SC,SD$$a.$ Chứng minh rằng $BC\bot (SAB),CD\bot (SAD)$$b.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $BD$$c.$ Chứng minh rằng $AH,AK$ cùng vuông góc với $SC$. Từ đó suy ra ba đường thẳng … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA$ vuông góc với mặt phẳng $(ABCD)$.Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên $SB,SC,SD$$a.$ Chứng minh rằng $BC\bot (SAB),CD\bot (SAD)$$b.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $BD$$c.$ Chứng minh rằng $AH,AK$ cùng vuông góc với $SC$. Từ đó suy ra ba đường thẳng $AH,AI,AK$ cùng chứa trong một mặt phẳng.$d.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $HK$. Từ đó suy ra $HK\bot AI$$e.$ Tính diện tích tứ giác $AHIK$ biết $SA=AB=a$

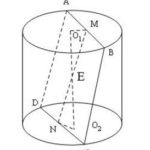
Đề bài: Bên trong hình trụ tròn xoay có một hình vuông $ABCD$ cạnh $a$ nội tiếp mà hai đỉnh liên tiếp $A, B$ nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng hình vuông tạo với đáy của hình trụ một góc $45^0$. Tính diện tích xung quanh và thể tích của hình trụ đó .

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Bên trong hình trụ tròn xoay có một hình vuông $ABCD$ cạnh $a$ nội tiếp mà hai đỉnh liên tiếp $A, B$ nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng hình vuông tạo với đáy của hình trụ một góc $45^0$. Tính diện tích xung quanh và thể tích của hình trụ đó . Lời giải Kí hiệu $O_1; O_2$ là … [Đọc thêm...] vềĐề bài: Bên trong hình trụ tròn xoay có một hình vuông $ABCD$ cạnh $a$ nội tiếp mà hai đỉnh liên tiếp $A, B$ nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng hình vuông tạo với đáy của hình trụ một góc $45^0$. Tính diện tích xung quanh và thể tích của hình trụ đó .

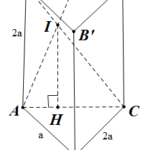
Đề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$. Lời giải Trong tam giác vuông $A'AC$ ta có:  $AC=\sqrt{9a^2-4a^2}=a\sqrt{5}$ Từ đó trong tam giác vuông $ABC$ thì :   … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$.

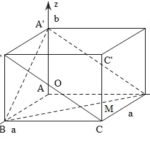
Đề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=a, AA'=b(a>0,b>0)$. Gọi $M$ là trung điểm cạnh $CC'$a) Tính thể tích khối tứ diện $BDA'M$ theo $a$ và $b$b) Xác định tỉ số $\frac{a}{b} $ để hai mặt phẳng $(A'BD)$ và $(MBD)$ và vuông góc với nhau

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=a, AA'=b(a>0,b>0)$. Gọi $M$ là trung điểm cạnh $CC'$a) Tính thể tích khối tứ diện $BDA'M$ theo $a$ và $b$b) Xác định tỉ số $\frac{a}{b} $ để hai mặt phẳng $(A'BD)$ và $(MBD)$ và vuông góc với nhau Lời giải a) Chọn hệ trục tọa độ $Oxyz$ như sau:- Gốc $O\equiv A$- Trục $Ox$ … [Đọc thêm...] vềĐề bài: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=a, AA'=b(a>0,b>0)$. Gọi $M$ là trung điểm cạnh $CC'$a) Tính thể tích khối tứ diện $BDA'M$ theo $a$ và $b$b) Xác định tỉ số $\frac{a}{b} $ để hai mặt phẳng $(A'BD)$ và $(MBD)$ và vuông góc với nhau

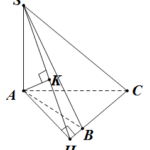
Đề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$. Lời giải Kẻ $AH \bot BC \Rightarrow SH \bot BC$ (định lí ba đường vuông góc).Lại có: $BC \bot (SAH)\Rightarrow (SBC)\bot (SAH)$.Do $(SBC) \cap (SAH)=AH,$nên nếu kẻ $AK \bot SH( K \in SH) \Rightarrow AK … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ có $SA=3a$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AB=BC=2a; \widehat{ABC}=120^0$ tìm khoảng cách từ $A$ đến mặt phẳng $(SBC)$.