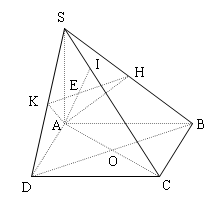

Lời giải

$a.$ Từ giả thiết :
$SA\bot (ABCD)\Rightarrow SA\bot BC (1)$
Mặt khác, ta có :
$AB\bot BC$ vì $ABCD$ là hình vuông $(2)$
Từ $(1),(2)$ suy ra $BC\bot (SAD)$
$b.$ Từ giả thiết :
$SA\bot (ABCD)\Rightarrow SA\bot BD (3)$
Mặt khác, ta có :
$AC\bot BD, $ vì $ABCD$ là hình vuông
Từ $(3),(4)$ suy ra :
$BD\bot (SAC)$ tại trung điểm $O$ của $BD$
Vậy $(SAC)$ là mặt trung trực của đoạn $BD$
$c.$ Từ giả thiết và kết hợp với kết quả câu $a.$ ta được :
$\begin{cases} AH\bot SB\\AH\bot BC\end{cases} \Leftrightarrow AH\bot (SBC)\Rightarrow AH\bot SC$
Chứng minh tương tự ta được $AK\bot SC$
Như vậy vì $AH,AI,AK$ cùng vuông góc với $SC$ nên ba đường thẳng $AH,AI,AK$ cùng chưa trong mặt phẳng qua $A$ và vuông góc với $SC$
$d.$ Giả sử $HK$ cắt $AI$ tại $E$
Nhận xét rằng :
$\Delta SAB=\Delta SAD (c.g.c)\Rightarrow SH\bot SK$
Trong $\Delta SBD$ ta có :
$\frac{SH}{SB}=\frac{SK}{SD}\Rightarrow HK//BD $ và $E$ là trung điểm của $HK$
Kết hợp với kết quả câu $a.$ suy ra :
$HK\bot (SAc)$ tại trung điểm $E$ của $HK$
Vậy $(SAC)$ là mặt phẳng trung trực của đoạn $HK$
Từ kết quả $HK\bot (SAC)$ suy ra $HK\bot AI$
$e.$ Ta có :
$S_{AHIK}=\frac{1}{2} AI.HK (5)$ trong đó :
– Trong $\Delta SAC$ vuông tại $A$ ta được :
$\frac{1}{AI^2}=\frac{1}{SA^2}+\frac{1}{AC^2}=\frac{1}{a^2} +\frac{1}{2a^2} \Rightarrow AI=\frac{a\sqrt{6} }{3} (6)$
– Trong $\Delta SBD$ ta được :
$\frac{SH}{SB} =\frac{SK}{SD}=\frac{1}{2} \Rightarrow HK$ là đường trung bình $\Rightarrow HK=\frac{a\sqrt{2} }{2} (7)$
Thay $(6),(7)$ vào $(5) $ ta được
$S_{AIHK}=\frac{1}{2} .\frac{a\sqrt{6} }{3} .\frac{a\sqrt{2} }{b} =\frac{a^2\sqrt{3} }{6} $
