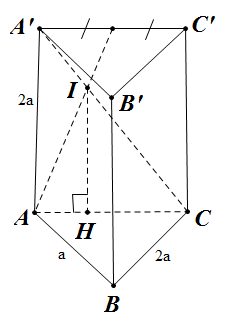
Đề bài: Cho hình lăng trụ $A'B'C'ABC$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a,AA'=2a; AC'=3a$. Gọi $M$ là trung điểm $A'C'$ và $I$ là giao điểm của $AM $ và $A'C$. Tính thể tích tứ diện $IABC$.

Lời giải

Trong tam giác vuông $A’AC$ ta có:
  $AC=\sqrt{9a^2-4a^2}=a\sqrt{5}$

Từ đó trong tam giác vuông $ABC$ thì :
   $BC=\sqrt{5a^2-a^2}=2a$.
Do $(AA’C’C) \bot (ABC)$ nên trong $(AA’C’C)$
kẻ $IH \bot AC (H \in AC)\Rightarrow IH \bot (ABC)$.
Theo định lí Talet ta có: $\frac{IH}{AA’}=\frac{CI}{CA’}$.
Vì $\frac{CI}{IA’}=\frac{AC}{A’M}=2\Rightarrow \frac{CI}{IA’+CI}=\frac{2}{3}\Rightarrow \frac{IH}{AA’}=\frac{CI}{CA’}=\frac{2}{3}\Rightarrow IH=\frac{2}{3}AA’=\frac{4a}{3}$
Ta có $V_{IABC}=\frac{1}{3}S_{ABC}.IH=\frac{1}{3}.\frac{1}{2}AB.BC.IH=\frac{1}{6}a.2a\frac{4a}{3}=\frac{4a^3}{9}$ (đvtt)