Hình học không gian

Đề bài: Cho $\alpha, \beta, \gamma$ là ba góc tạo bởi đường chéo hình hộp chữ nhật với ba cạnh xuất phát từ một điểm. Chứng minh:a) $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$b) $\sqrt{4cos^2\alpha+1}+\sqrt{4\cos^2\beta+1}+\sqrt{4\cos^2\gamma+1}\leq \sqrt{21}$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

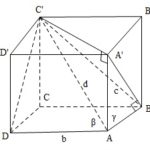
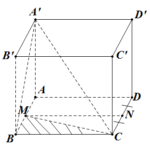
Đề bài: Cho $\alpha, \beta, \gamma$ là ba góc tạo bởi đường chéo hình hộp chữ nhật với ba cạnh xuất phát từ một điểm. Chứng minh:a) $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$b) $\sqrt{4cos^2\alpha+1}+\sqrt{4\cos^2\beta+1}+\sqrt{4\cos^2\gamma+1}\leq \sqrt{21}$ Lời giải a) Chứng minh: $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$Giả sử cho hình hộp chữ nhật $ABCD.A'B'C'D'$ … [Đọc thêm...] vềĐề bài: Cho $\alpha, \beta, \gamma$ là ba góc tạo bởi đường chéo hình hộp chữ nhật với ba cạnh xuất phát từ một điểm. Chứng minh:a) $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$b) $\sqrt{4cos^2\alpha+1}+\sqrt{4\cos^2\beta+1}+\sqrt{4\cos^2\gamma+1}\leq \sqrt{21}$

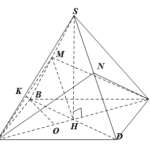
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh bên và cạnh đáy đều bằng $a$. Có một hình cầu đi qua $A$ và tiếp xúc với $SB,SD$ tại các trung điểm của chúng. Xác định tâm $O$ của hình cầu và tính bán kính của hình cầu ấy theo $a$.

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh bên và cạnh đáy đều bằng $a$. Có một hình cầu đi qua $A$ và tiếp xúc với $SB,SD$ tại các trung điểm của chúng. Xác định tâm $O$ của hình cầu và tính bán kính của hình cầu ấy theo $a$. Lời giải Gọi $M$ là trung điểm của $SB$. Vì hình cầu tiếp xúc với $SB$ tại trung điểm của $SB$ nên $OM \bot SB \Rightarrow O \in $ … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh bên và cạnh đáy đều bằng $a$. Có một hình cầu đi qua $A$ và tiếp xúc với $SB,SD$ tại các trung điểm của chúng. Xác định tâm $O$ của hình cầu và tính bán kính của hình cầu ấy theo $a$.

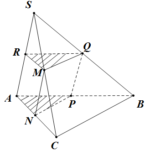
Đề bài: Cho hình chóp $S.ABC$. Gọi $M$ là trung điểm của $SB$. Dựng thiết diện với hình chóp qua $M, $song song với $SA,BC$. Chứng minh thiết diện chia khôi chóp thành hai phần bằng nhau.

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Thể tích khối đa diện

Đề bài: Cho hình chóp $S.ABC$. Gọi $M$ là trung điểm của $SB$. Dựng thiết diện với hình chóp qua $M, $song song với $SA,BC$. Chứng minh thiết diện chia khôi chóp thành hai phần bằng nhau. Lời giải Kẻ $MN // SA (N \in AB), MQ// BC (Q\in SC)$Kẻ $NP// BC (P\in AC)\Rightarrow QP //SA $.Thiết diện là hình bình hành $MNQP$. Dễ thấy $M,N,Q,P$ lần lượt là trung điểm của … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$. Gọi $M$ là trung điểm của $SB$. Dựng thiết diện với hình chóp qua $M, $song song với $SA,BC$. Chứng minh thiết diện chia khôi chóp thành hai phần bằng nhau.

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $AD, BB'$a) Chứng minh: $MN\bot A'C$b) Tìm góc hợp bởi hai đường thẳng $MN$ và $AC'$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $AD, BB'$a) Chứng minh: $MN\bot A'C$b) Tìm góc hợp bởi hai đường thẳng $MN$ và $AC'$ Lời giải Chọn hệ trục tọa độ như hình vẽ.Khi đó: $A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0), A'(0;0;a), B'(a;0;a), C'(a;a;a), D'(0;a;a), … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $AD, BB'$a) Chứng minh: $MN\bot A'C$b) Tìm góc hợp bởi hai đường thẳng $MN$ và $AC'$

Đề bài: Cho hình lập phương $ABCD.A_{1}B_{1}C_{1}D_{1}$ có tâm $O$,gọi $I$ là tâm của mặt $CDD_{1}C_{1}$.Hãy phân tích các vectơ $\overrightarrow {AO},\overrightarrow {AI}$ theo ba vectơ $\overrightarrow {AB},\overrightarrow {AD},\overrightarrow {AA_{1}}$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Vectơ trong không gian

Đề bài: Cho hình lập phương $ABCD.A_{1}B_{1}C_{1}D_{1}$ có tâm $O$,gọi $I$ là tâm của mặt $CDD_{1}C_{1}$.Hãy phân tích các vectơ $\overrightarrow {AO},\overrightarrow {AI}$ theo ba vectơ $\overrightarrow {AB},\overrightarrow {AD},\overrightarrow {AA_{1}}$ Lời giải cần giải chi tiết … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A_{1}B_{1}C_{1}D_{1}$ có tâm $O$,gọi $I$ là tâm của mặt $CDD_{1}C_{1}$.Hãy phân tích các vectơ $\overrightarrow {AO},\overrightarrow {AI}$ theo ba vectơ $\overrightarrow {AB},\overrightarrow {AD},\overrightarrow {AA_{1}}$

Đề bài: Cho hình chóp $S.ABCD$ đáy là hình thoi cạnh $AB=\sqrt{5}$, đường chéo $AC=4, SO=2\sqrt{2}$; và $SO$ vuông góc với mặt đáy $(ABCD)$, ở đây, $O$ là giao điểm của $AC,BD$. Gọi $M$ là trung điểm của cạnh $SC$. Tìm khoảng cách giữa hai đường thẳng $SA,BM$.

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình chóp $S.ABCD$ đáy là hình thoi cạnh $AB=\sqrt{5}$, đường chéo $AC=4, SO=2\sqrt{2}$; và $SO$ vuông góc với mặt đáy $(ABCD)$, ở đây, $O$ là giao điểm của $AC,BD$. Gọi $M$ là trung điểm của cạnh $SC$. Tìm khoảng cách giữa hai đường thẳng $SA,BM$. Lời giải Ta có: $MO//SA\Rightarrow SA \bot (OMB)$$\Rightarrow d(SA,BM)=d(SA,(MOB))=d(S,(MOB))=d(C,(MOB)) … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ đáy là hình thoi cạnh $AB=\sqrt{5}$, đường chéo $AC=4, SO=2\sqrt{2}$; và $SO$ vuông góc với mặt đáy $(ABCD)$, ở đây, $O$ là giao điểm của $AC,BD$. Gọi $M$ là trung điểm của cạnh $SC$. Tìm khoảng cách giữa hai đường thẳng $SA,BM$.

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$ Lời giải Ta có $MN// BC\Rightarrow MN// (A'BC)$ $\Rightarrow d(MN, A'C)=d(MN, (A'BC))=D(M,(A'BC)) (1)$Dễ thấy … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$

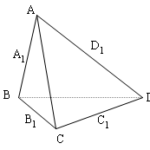
Đề bài: Cho tứ diện $ABCD$.Gọi $A_1,B_1,C_1,D_1$ là các điểm thỏa mãn :$\overrightarrow {A_1A}=-2\overrightarrow {A_1B}, \overrightarrow {B_1B}=-2\overrightarrow {B_1C} $$\overrightarrow {C_1C}=-2\overrightarrow {C_1D} , \overrightarrow {D_1D}=-2\overrightarrow {D_1A} $Đặt $\overrightarrow {AB}=\overrightarrow {i},\overrightarrow {AC}=\overrightarrow {j} ,\overrightarrow {AD}=\overrightarrow {k} $.Hãy biểu diễn các véctơ $\overrightarrow {A_1B_1},\overrightarrow {A_1C_1},\overrightarrow {A_1D_1} $ theo ba véctơ $\overrightarrow {i},\overrightarrow {j},\overrightarrow {k} $

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Vectơ trong không gian

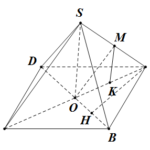
Đề bài: Cho tứ diện vuông $OABC$,vuông tại $O$ và $OA=OB=OC$.Điểm $M$ thỏa mãn $|\overrightarrow {OM}|=OA$,nửa đường thẳng $OM$ tạo với tia $OC$ một góc bẳng $45^{0}$ và tạo với hai tia $OA,OB$ thành hai góc nhọn bằng nhau.Hãy phân tích vectơ $\overrightarrow {OM}$ theo ba vectơ $\overrightarrow {OA},\overrightarrow {OB},\overrightarrow {OC}$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Vectơ trong không gian

Đề bài: Cho tứ diện vuông $OABC$,vuông tại $O$ và $OA=OB=OC$.Điểm $M$ thỏa mãn $|\overrightarrow {OM}|=OA$,nửa đường thẳng $OM$ tạo với tia $OC$ một góc bẳng $45^{0}$ và tạo với hai tia $OA,OB$ thành hai góc nhọn bằng nhau.Hãy phân tích vectơ $\overrightarrow {OM}$ theo ba vectơ $\overrightarrow {OA},\overrightarrow {OB},\overrightarrow {OC}$ Lời giải cần … [Đọc thêm...] vềĐề bài: Cho tứ diện vuông $OABC$,vuông tại $O$ và $OA=OB=OC$.Điểm $M$ thỏa mãn $|\overrightarrow {OM}|=OA$,nửa đường thẳng $OM$ tạo với tia $OC$ một góc bẳng $45^{0}$ và tạo với hai tia $OA,OB$ thành hai góc nhọn bằng nhau.Hãy phân tích vectơ $\overrightarrow {OM}$ theo ba vectơ $\overrightarrow {OA},\overrightarrow {OB},\overrightarrow {OC}$

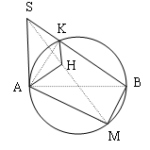
Đề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$

Ngày 24/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$ Lời giải Nhận thấy mặt phẳng $SBM$ chứa đường thẳng $SB$ cố định.Ta đi dựng mặt phẳng qua $A$ và vuông góc với $SB$ bằng cách :- Trong $(SAB)$ … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$