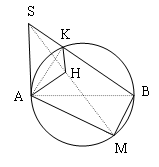
Đề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$

Lời giải

Nhận thấy mặt phẳng $SBM$ chứa đường thẳng $SB$ cố định.Ta đi dựng mặt phẳng qua $A$ và vuông góc với $SB$ bằng cách :
– Trong $(SAB)$ hạ $AK\bot SB$
– Trong $(SBM)$ dựng $Kx\bot SB$ và cắt $SM$ tại $H$
Khi đó :
$(AKH)\bot SB$ và $(AKH)\cap (SBM)=KH$
TA đi chứng minh $AH\bot (SBM)$ thật vậy :
$\begin{cases} BM\bot AM\\BM\bot SA\end{cases} \Leftrightarrow  BM\bot (SAM)\Rightarrow  BM\bot AH\Rightarrow  AH\bot (ABM)$
Trong $(AKH)$ ta có :
$AH\bot HK\Leftrightarrow  \widehat{AHK} =90^0$
nên $H$ thuộc đường tròn đường kính $AK$ trong mặt phẳng $(AKH)$