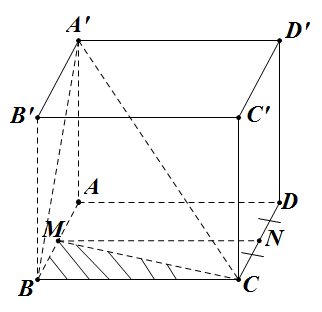
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tính khoảng cách giữa hai đường thẳng $A'C, MN$

Lời giải

Ta có $MN// BC\Rightarrow MN// (A’BC)$
  $\Rightarrow d(MN, A’C)=d(MN, (A’BC))=D(M,(A’BC))  (1)$

Dễ thấy $V_{A’MBC}=\frac{1}{3}S_{MBC}.AA’=\frac{1}{3}.\frac{1}{2}.1.1.1=\frac{1}{12}   $
Vì $CB \bot (BAA’B’)\Rightarrow CB \bot BA’$
$\Rightarrow A’BC$ là tam giác vuông tại $B$.
Từ đó : $V_{A’.MBC}=V_{M.A’BC}=\frac{1}{3}.S_{A’BC}.h (2)$
Từ $(1),(2)$ ta có:
   $\frac{1}{12}=\frac{1}{3}.\frac{1}{2}A’B.BC.h=\frac{1}{6}\sqrt{2}h\Rightarrow h=\frac{\sqrt{2}}{4}  (3)$
Từ $(1),(2),(3)$ suy ra: $d(MN,A’C)=\frac{\sqrt{2}}{4}  $.