Hình học không gian

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác $ABC$ với $AB=AC, \widehat{BAC}=\alpha $. Gọi $M$ là trung điểm của $AA'$ và giả sử mặt phẳng $(C'MB)$ tạo với đáy $(ABC)$ một góc $\beta$.1. Chứng minh $\widehat{C'BC}=\beta$.2. Chứng minh $\tan \frac{\alpha}{2}= \cos \beta$ là điều kiện cần và đủ để $BM\bot MC'$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác $ABC$ với $AB=AC, \widehat{BAC}=\alpha $. Gọi $M$ là trung điểm của $AA'$ và giả sử mặt phẳng $(C'MB)$ tạo với đáy $(ABC)$ một góc $\beta$.1. Chứng minh $\widehat{C'BC}=\beta$.2. Chứng minh $\tan \frac{\alpha}{2}= \cos \beta$ là điều kiện cần và đủ để $BM\bot MC'$. Lời giải … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác $ABC$ với $AB=AC, \widehat{BAC}=\alpha $. Gọi $M$ là trung điểm của $AA'$ và giả sử mặt phẳng $(C'MB)$ tạo với đáy $(ABC)$ một góc $\beta$.1. Chứng minh $\widehat{C'BC}=\beta$.2. Chứng minh $\tan \frac{\alpha}{2}= \cos \beta$ là điều kiện cần và đủ để $BM\bot MC'$.

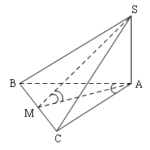
Đề bài: Từ một điểm $S$ ngoài mặt phẳng $(P)$ ta kẻ đường thẳng $SA$ vuông góc với mặt phẳng $(P)$ và nối $S$ với hai điểm phân biệt $B,C$ thuộc mặt phẳng $(P)$.Các đường thẳng $SB,SC$ tạo với mặt phẳng $(P)$ các góc $45^0$ và tạo với nhau góc $60^0$$a.$ Chứng minh hai mặt phẳng $(SAB),(SAC)$ vuông góc với nhau$b.$ Tính góc giữa các mặt phẳng $(SBC),(P)$

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Từ một điểm $S$ ngoài mặt phẳng $(P)$ ta kẻ đường thẳng $SA$ vuông góc với mặt phẳng $(P)$ và nối $S$ với hai điểm phân biệt $B,C$ thuộc mặt phẳng $(P)$.Các đường thẳng $SB,SC$ tạo với mặt phẳng $(P)$ các góc $45^0$ và tạo với nhau góc $60^0$$a.$ Chứng minh hai mặt phẳng $(SAB),(SAC)$ vuông góc với nhau$b.$ Tính góc giữa các mặt phẳng $(SBC),(P)$ Lời giải … [Đọc thêm...] vềĐề bài: Từ một điểm $S$ ngoài mặt phẳng $(P)$ ta kẻ đường thẳng $SA$ vuông góc với mặt phẳng $(P)$ và nối $S$ với hai điểm phân biệt $B,C$ thuộc mặt phẳng $(P)$.Các đường thẳng $SB,SC$ tạo với mặt phẳng $(P)$ các góc $45^0$ và tạo với nhau góc $60^0$$a.$ Chứng minh hai mặt phẳng $(SAB),(SAC)$ vuông góc với nhau$b.$ Tính góc giữa các mặt phẳng $(SBC),(P)$

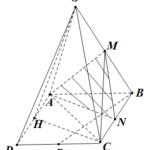
Đề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$ Lời giải Gọi $H$ là trung điểm của $AD$ do $SAD$ là tam giác đều , nên $SH \bot AD$.Vì $(SAD) \bot (ABCD)\Rightarrow SH \bot (ABCD)\Rightarrow SH \bot BP … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$

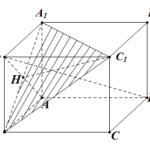
Đề bài: Cho hình lập phương $ABCD.A_1B_1C_1D_1$ cạnh $a$. Tìm khoảng cách giữa hai đường thẳng $A_1B; B_1D$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình lập phương $ABCD.A_1B_1C_1D_1$ cạnh $a$. Tìm khoảng cách giữa hai đường thẳng $A_1B; B_1D$. Lời giải Ta có: $A_1B\bot B_1A (BAA_1B_1$ là hình vuông ); $A_1B \bot AD $( vì $AD \bot (BAA_1B_1)$)$\Rightarrow A_1B \bot (B_1AD) \Rightarrow A_1B\bot B_1D (1)$Vì $DD_1 \bot (A_1B_1C_1D_1) \Rightarrow DD_1 \bot A_1C_1$.Do $A_1B_1C_1D_1$ là hình vuông nên … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A_1B_1C_1D_1$ cạnh $a$. Tìm khoảng cách giữa hai đường thẳng $A_1B; B_1D$.

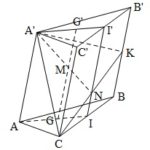
Đề bài: Cho lăng trụ tam giác $ABCA'B'C'$. $G$ và $G'$ là trọng tâm hai đáy. Qua trung điểm $M$ của $GG'$ kẻ một đường thẳng song song $CA'$, nó cắt mặt $ABB'A'$ và $BCC'A'$ tại $F, E$. Tìm độ dài $FE$ biết $CA'=a$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he song song

Đề bài: Cho lăng trụ tam giác $ABCA'B'C'$. $G$ và $G'$ là trọng tâm hai đáy. Qua trung điểm $M$ của $GG'$ kẻ một đường thẳng song song $CA'$, nó cắt mặt $ABB'A'$ và $BCC'A'$ tại $F, E$. Tìm độ dài $FE$ biết $CA'=a$. Lời giải Kẻ các đường trung tuyến $AI$ và $A'I'$ thì $G$ và $G'$ thuộc các đường này. Trong mp … [Đọc thêm...] vềĐề bài: Cho lăng trụ tam giác $ABCA'B'C'$. $G$ và $G'$ là trọng tâm hai đáy. Qua trung điểm $M$ của $GG'$ kẻ một đường thẳng song song $CA'$, nó cắt mặt $ABB'A'$ và $BCC'A'$ tại $F, E$. Tìm độ dài $FE$ biết $CA'=a$.

Đề bài: Cho $n$ điểm $A_1, A_2,…A_n$ và $n$ số $k_1, k_2,…, k_n$ mà $k_1+k_2+…+k_n=k$a) Chứng minh rằng có duy nhất một điểm $G$ sao cho:$k_1 \overrightarrow{GA_1}+k_2 \overrightarrow{GA_2}+…+k_n \overrightarrow{GA_n}=\overrightarrow{0}$Điểm $G$ như thế gọi là tâm tỉ cự của hệ điểm $A_i$, gắn với các hệ số $k_i$. Trong trường hợp các hệ số $k_i$ bằng nhau (và do đó có thể xem các $k_i$ đều bằng 1) thì $G$ gọi là trọng tâm của hệ điểm $A_i$.b) Chứng minh rằng nếu $G$ là tâm tỉ cự nói ở câu a) thì với mọi điểm $O$ bất kì, ta có: $\overrightarrow{OG}=\frac{1}{k}(k_1 \overrightarrow{OA_1}+k_2 \overrightarrow{OA_2}+…+k_n \overrightarrow{OA_n})$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Vectơ trong không gian

Đề bài: Cho $n$ điểm $A_1, A_2,...A_n$ và $n$ số $k_1, k_2,..., k_n$ mà $k_1+k_2+...+k_n=k$a) Chứng minh rằng có duy nhất một điểm $G$ sao cho:$k_1 \overrightarrow{GA_1}+k_2 \overrightarrow{GA_2}+...+k_n \overrightarrow{GA_n}=\overrightarrow{0}$Điểm $G$ như thế gọi là tâm tỉ cự của hệ điểm $A_i$, gắn với các hệ số $k_i$. Trong trường hợp các hệ số $k_i$ bằng nhau (và do đó có … [Đọc thêm...] vềĐề bài: Cho $n$ điểm $A_1, A_2,…A_n$ và $n$ số $k_1, k_2,…, k_n$ mà $k_1+k_2+…+k_n=k$a) Chứng minh rằng có duy nhất một điểm $G$ sao cho:$k_1 \overrightarrow{GA_1}+k_2 \overrightarrow{GA_2}+…+k_n \overrightarrow{GA_n}=\overrightarrow{0}$Điểm $G$ như thế gọi là tâm tỉ cự của hệ điểm $A_i$, gắn với các hệ số $k_i$. Trong trường hợp các hệ số $k_i$ bằng nhau (và do đó có thể xem các $k_i$ đều bằng 1) thì $G$ gọi là trọng tâm của hệ điểm $A_i$.b) Chứng minh rằng nếu $G$ là tâm tỉ cự nói ở câu a) thì với mọi điểm $O$ bất kì, ta có: $\overrightarrow{OG}=\frac{1}{k}(k_1 \overrightarrow{OA_1}+k_2 \overrightarrow{OA_2}+…+k_n \overrightarrow{OA_n})$.

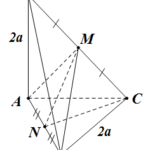
Đề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Khoảng cách trong không gian

Đề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$. Lời giải Gọi $M,N$ lần lượt là trung điểm của $SC,AB$.ta có: $MA=MB=\frac{SC}{2}\Rightarrow MN \bot AB$.Dễ thấy tam giác vuông $SAN$ bằng tam giác vuông $NBC\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B, AB=a, BC=2a$, cạnh $SA$ vuông góc với đáy và $SA=2a$. Xác định và tính độ dài đường vuông góc chung của hai đường thẳng $AB,SC$.

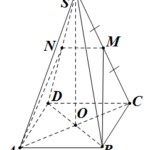
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Thể tích khối đa diện

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$ Lời giải Normal 0 false … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5} cm$, đường chéo $AC=4 cm$. Đoạn thẳng $SO=2\sqrt{2} cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$

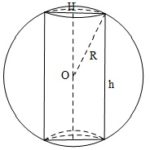
Đề bài: Một hình trụ nội tiếp một hình cầu, có tỉ số giữa diện tích toàn phần của hình trụ và diện tích hình cầu bằng $m$. Xác định tỉ số giữa bán kính đáy của hình trụ và bán kính hình cầu để $m$ lớn nhất.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

Đề bài: Một hình trụ nội tiếp một hình cầu, có tỉ số giữa diện tích toàn phần của hình trụ và diện tích hình cầu bằng $m$. Xác định tỉ số giữa bán kính đáy của hình trụ và bán kính hình cầu để $m$ lớn nhất. Lời giải Giả sử bán kính hình cầu bằng $R$, bán kính hình trụ bằng $r$, đường cao hình trụ bằng $h$.Ta có: $h=2OH=2\sqrt{R^2-r^2}=2R\sqrt{1-\frac{r^2}{R^2}}$Ta … [Đọc thêm...] vềĐề bài: Một hình trụ nội tiếp một hình cầu, có tỉ số giữa diện tích toàn phần của hình trụ và diện tích hình cầu bằng $m$. Xác định tỉ số giữa bán kính đáy của hình trụ và bán kính hình cầu để $m$ lớn nhất.

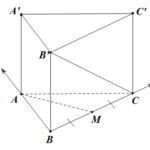
Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$, cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tìm khoảng cách giữa hai đường thẳng $AM,B'C$.

Ngày 26/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Mặt tròn xoay

Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$, cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tìm khoảng cách giữa hai đường thẳng $AM,B'C$. Lời giải Vì $ABC.A'B'C'$ là hình lăng trụ đứng và $\widehat{ABC}=90^0$ nên ta dựng hệ trục tọa độ như hình vẽ với gốc tọa độ là $B$.Trong hệ trục tọa độ này … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ đáy là tam giác vuông có $BA=BC=a$, cạnh bên $AA'=a\sqrt{2}$. Gọi $M$ là trung điểm của $BC$. Tìm khoảng cách giữa hai đường thẳng $AM,B'C$.