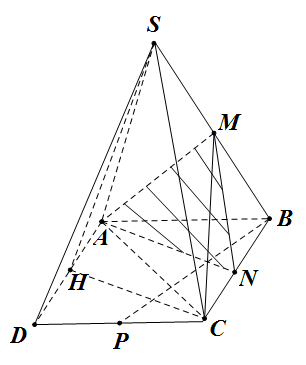
Đề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$

Lời giải

Gọi $H$ là trung điểm của $AD$ do $SAD$ là tam giác đều , nên $SH \bot AD$.

Vì $(SAD) \bot (ABCD)\Rightarrow SH \bot (ABCD)\Rightarrow SH \bot BP (1)$
Dễ thấy hai tam giác vuông $BPC, CHD$ là bằng nhau, nên ta có:
  $\widehat{B_1}=\widehat{C_1}\Rightarrow \widehat{B_1}+\widehat{C_2}=\widehat{C_1}\widehat{C_2}=90^0$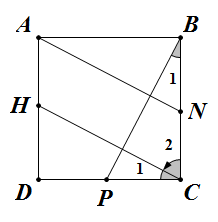

   $\Rightarrow BP \bot CH   (2)$
Từ $(1),(2)$ suy ra $BP \bot (SHC)   (3)$
Do $HC// AN, MN// SC\Rightarrow (SHC)//(MAN) (4)$
Từ $(3),(4) $ suy ra $BP \bot (MAN)$
$\Rightarrow AM \bot BP $ (đpcm)