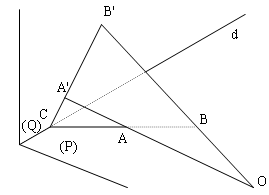
Đề bài: Cho hai mặt phẳng $(P), (Q)$ cắt nhau theo giao tuyến $d$. Cho $A, B$ là hai điểm thuộc $d$. Gọi $O$ là điểm tùy ý nằm ngoài $(P), (Q)$. Giả sử các đường thẳng $OA, OB$ lần lượt cắt $(Q)$ tại $A'$ và đường thẳng $AB$ cắt $d$ tại $C$.a) Ba điểm $O, A, B$ có thể thẳng hàng không, tại sao?b) Chứng minh ba đường thẳng $AB, A'B'$ và $d$ đồng quy.

Lời giải

 
a) Ba điểm $O, A, B$ không thể thẳng hàng. Thật vậy, nếu chúng thẳng hàng thì $O$ nằm trên đường thẳng $AB$, nên $O$ phải thuộc mặt phẳng $(P)$, điều này trái giả thiết.
b) Xét hai mặt phẳng $(OAB)$ và mặt phẳng $(Q)$: Do $C$ là giao điểm của $d$ (nằm trong $(Q)$) và $AB$ (nằm trong $(OAB)$) nên $C$ là điểm chung của $(Q)$ và $(OAB)$. Theo giả thiết, các đường thẳng $OA, OB$ lần lượt cắt $(Q)$ tại $A’$ và $B’$, nên ta cũng có $A’, B’$ cũng là những điểm chung của $(OAB)$ và $(Q)$.
Vậy ba điểm $C, A’, B’$ cùng thuộc giao tuyến của $(OAB)$ và $(Q)$, nên chúng thẳng hàng. Từ đó suy ra rằng ba đường thẳng $AB, A’B’$ và $d$ đồng quy tại $C$.