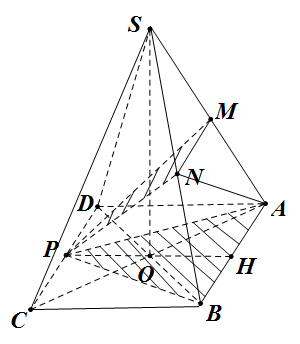
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$.

Lời giải

 Do $MS=MA\Rightarrow d(A,(MNP))=d(S,(MNP))  (1) \Rightarrow V_{A.MNP}=V_{S.MNP}$
Theo bài toán cơ bản, ta có:
$\frac{V_{SMNP}}{V_{S.ABP}}=\frac{SM}{SA}.\frac{SN}{SB}=\frac{1}{4}\Rightarrow V_{S.MNP}=\frac{1}{4}.\frac{1}{3}S_{ABP}.SO=\frac{1}{4}.\frac{1}{3}.\frac{1}{2}AB.HP.SO$
                                   $=\frac{1}{24}a.a.\sqrt{a^2-\frac{a^2}{2}}=\frac{a^3\sqrt{6}}{48}    (2)$
Từ $(1),(2)$ suy ra : $V_{A.MNP}=\frac{a^3\sqrt{6}}{48}$ (đvtt).