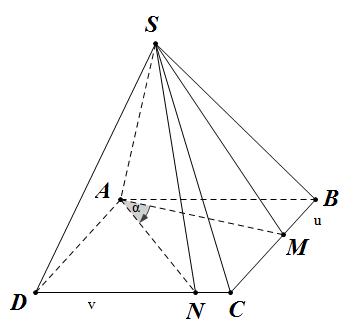
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Đoạn $SA$ cố định vuông góc với $(P)$ tại $A$. $M,N$ lần lượt là các điểm di động trên cạnh $BC$ và $CD$. Đặt $BM=u, DN=v$. Chứng minh rằng $a(u+v)+uv=a^2$ là điều kiện cần và đủ để hai mặt phẳng $(SAM),(SAN)$ tạo với nhau một góc $45^0$.

Lời giải

ta có: $(SAM) \cap (SAN)=SA$
Vì $SA\bot (ABCD)\Rightarrow AM \bot SA, AN\bot SA$.
Do vậy $\widehat{MAN}=\alpha$ là góc giữa hai mặt phẳng $(SAM),(SAN)$. Từ đó:
$\alpha =45^0\Leftrightarrow \widehat{NAD}+\widehat{BAM}=45^0$
$\Leftrightarrow \tan (\widehat{NAD}+\widehat{BAM})=1$
$\Leftrightarrow \frac{\tan \widehat{NAD}+\tan \widehat{BAM}}{1-\tan \widehat{NAD}.\tan \widehat{BAM}}=1\Leftrightarrow \frac{\frac{v}{u}+\frac{u}{a}}{1-\frac{uv}{a^2}}=1\Leftrightarrow a(u+a)+uv=a^2\Rightarrow $ đpcm.