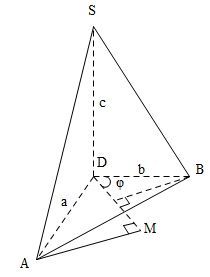
Đề bài:     Cho tứ diện $ABCD$, trong đó góc tam diện đỉnh $D$ là tam diện vuông. Giả sử $DA=a, DB=b, DC=c$. Chứng minh rằng với mỗi điểm $M$ nằm trên một cạnh  của $\triangle ABC$ thì:    $S=d(A,DM)+d(B,DM)+d(C,DM) \leq \sqrt{2(a^2+b^2+c^2)}$Khi nào xảy ra dấu bằng, ở đây $d(A,DM)$ là khoảng cách từ $A$ đến $DM$.

Không giảm tổng quát ta có thể giả sử $A$ nằm trên $AB$
Đặt $MDB=\varphi$. Khi đó dễ dàng ta thấy $S=c+a\cos \varphi+b\sin \varphi$
Theo bất đẳng thức Bu-nhi-a-cốp-xki, ta có:
   $a\cos \varphi+b\sin \varphi \leq \sqrt{a^2+b^2}   (1)$
Dấu bằng trong $(1)$ có $\Leftrightarrow  \frac{a}{\cos \varphi}=\frac{b}{\sin \varphi} \Leftrightarrow \tan \varphi=\frac{b}{a}$
Chú ý là trong tam giác vuông $ADB$ thì $\frac{b}{a}=\tan DAB $ từ đó suy ra dấu bằng trong $(1) \Leftrightarrow \varphi =DAB \Leftrightarrow DM \bot AB$
Vậy ta có: $S \leq c+\sqrt{a^2+b^2}$
Lại áp dụng bất đẳng thức Bu-nhi-a-cốp-xki, ta có: $S \leq \sqrt{2(A^2+b^2+c^2)}  (2) \Rightarrow$ điều phải chứng minh
Dấu bằng trong $(2)$ có $\Leftrightarrow DM\bot AB$ và $c=\sqrt{a^2+b^2}$