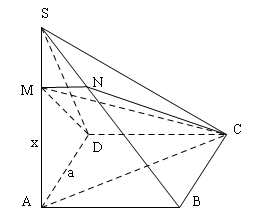
Đề bài: Cho chóp $S.ABCD$ có đáy $ABCD$  là hình vuông cạnh $a,SA\bot (ABCD);SA=a$. Mặt phẳng $(P)$ đi qua $CD$ cắt $SA,SB$ lần lượt tại $M,N$. Đặt $AM=x$. Tứ giác $MNCD$ là hình gì ? Tính diện tích tứ giác đó theo $a,x$

Lời giải

Ta có : $DC//AB\Rightarrow  DC//(SAB)$
$\Rightarrow  mp(MDC)\cap mp(SAB)=MN//AB$.Lại có $MN\bot (SAD)$.Suy ra tứ giác $MNCD$ là hình thang vuông.
Diện tích $MNCD$ là :
$S_{MNCD}=\frac{1}{2} (MN+CD)MD$
Trong đó : $CD=a$
$MD=\sqrt{MA^2+AD^2} =\sqrt{x^2+a^2} $
Trong $\Delta SAB$ ta có $MN//AB$ suy ra
$\frac{MN}{AB}=\frac{SM}{SA}\Rightarrow  \frac{MN}{a}   =\frac{a-x}{a} \Rightarrow  MN=a-x$
Do đó $S_{MNCD}=\frac{1}{2}\sqrt{x^2+a^2}.(a+a-x)=\frac{1}{2}   \sqrt{x^2+a^2}(2a-x) $