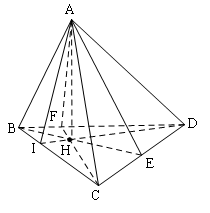
Đề bài: Chứng minh rằng trong một tứ diện, nếu có hai cặp đối diện vuông góc thì cặp cạnh đối diện còn lại cũng vuông góc

Lời giải

Tứ diện $ABCD$ có $AB\bot CD$ và $AD\bot BC.$Ta cần chứng minh $AC\bot BD$.Từ $A$ kẻ $AE\bot CD$.Kết hợp với $AB\bot CD$ ta suy ra $CD\bot (AEB)$
Ta lại có $CD\subset  (BCD)$ nên ta được $(AEB)\bot (BCD)      (1)$
Tương tự, nếu kẻ $AI\bot BC$ thì $(AID)\bot (BCD)        (2)$
Gọi $AH=(AEB)\cap (AID)       (3)$
Từ $(1),(2),(3)$ suy ra
$AH\bot (BCD)\Rightarrow  AH\bot BD     (4)$
Trong tam giác $BCD,BE\bot CD$ và $DI\bot BC$ nên $H$ là trực tâm của $\Delta BCD$ suy ra
$CH\bot BD       (5)$
Từ $(4),(5)$ suy ra
$BD\bot (ACH)$
Kết hợp với $AC\subset  (ACH)$ suy ra $AC\bot BD$