Đề bài: Cho hình chóp $S.ABCD$ có $SA=a\sqrt{6} $ và vuông góc với mặt phẳng $(ABCD)$ đáy $ABCD$ là nửa lục giác đều nội tiếp trong đường tròn đường kính $AD=2a$$a.$ Tính các khoảng cách từ $A$ và $B$ đến mặt phẳng $(SCD)$$b.$ Tính khoảng cách từ đường thẳng $AD$ đến mặt phẳng $(SBC)$$c.$ Tính diện tích của thiết diện của hình  chóp $S.ABCD$ với mặt phẳng $(\alpha) $ song song với mặt phẳng $(SAD)$ và cách một khoảng bằng $\frac{a\sqrt{3} }{4} $

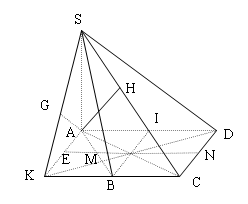
Lời giải

$a.$ Nhận xét rằng :
$\begin{cases}CD\bot AC\\CD\bot SA \end{cases}  \Rightarrow  CD\bot (SAC)\Rightarrow  (SCD)\bot (SAC)$
Hạ $AH$ vuông góc với $SC$ ta có ngay $AH\bot (SCD)$
Vậy $AH$ vuông góc với $SC$ ta có ngay $AH\bot (SCD)$
Trong $\Delta SAB$ vuông tại $A$ ta có:
$\frac{1}{AH^2} =\frac{1}{SA^2}+\frac{1}{AC^2}=\frac{1}{(a\sqrt{6} )^2}+\frac{1}{(a\sqrt{3} )^2}=\frac{1}{2a^2}     \Rightarrow  AH=a\sqrt{2} $
Gọi $I$ là trung điểm $AD$ suy ra :
$BI//CD\Rightarrow  BI//(SCD)\Rightarrow  d(B,(SCD))=d(I,(SCD))$
Mặt khác, ta lại có $AI\cap (SCD)$ nên :
$\frac{d(I,(SCD))}{d(A,(SCD))} =\frac{ID}{AD} =\frac{1}{2} \Rightarrow  d(I,(SCD))=\frac{1}{2} d(A,(SCD))=\frac{1}{2} AH=\frac{a\sqrt{2} }{2} $
$B.$ Nhận xét rằng :
$AD//CD\Rightarrow  AD//(SBC)\Rightarrow  d(AD,(SBC))=d(A,(SBC))$
Hạ $AK$ vuông góc với $BC$ ta được :
$\begin{cases} BC\bot AK\\BC\bot SA\end{cases} \Rightarrow  BC\bot (SAK)\Rightarrow  (SBC)\bot (SAK)$ và $(SBC)\cap (SAK)=AK$
Hạ $AG$ vuông góc với $SK$ ta có ngay $AG\bot (SBC)$
Vậy $AG$ là khoảng cácg từ điểm $A$ tới $SBC$
Trong $\Delta SAK$ vuông tại $A$ ta có :
$\frac{1}{AG^2}=\frac{1}{SA^2}+\frac{1}{AK^2}=\frac{1}{(a\sqrt{6} )^2} +\frac{1}{(\frac{a\sqrt{3} }{2} )^2}    =\frac{3}{2a^2}\Rightarrow  AG=\frac{a\sqrt{6} }{3}  $
$c.$ Nhận xét rằng :
$\begin{cases} AK\bot AD\\AK\bot SA\end{cases} \Rightarrow  AK\bot (SAD)$
Giả sử mặt phẳng $\alpha $ song song với mặt phẳng $(SAD)$ cắt $AK$ tại $E$ khi đó :
$d(\alpha ,(SAD))=AE=\frac{a\sqrt{3} }{4} =\frac{1}{2} AK\Rightarrow  E$ là trung điểm của $AK$
Ta đi xác định thiết diện tạo bởi hình chóp với mặt phẳng $\alpha $ qua $E$ và song song với $(SAD)$ như sau :
$\begin{cases}\alpha //(SAD) \\\alpha \cap (ABCD)=Ex\\(SAD)\cap (ABCD)=AD\end{cases} \Rightarrow  Ex//AD$
và $Ex$ cắt $AB,CD$ theo thứ tự tại $M,N$ là trung điểm của mỗi đoạn
Trong mặt phẳng $(SAB)$ dựng $My//SA$ và cắt $SB$ tại $Q$ là trung điểm của $SB$
Trong mặt phẳng $(SCD)$ dựng $Nz,SD$ và cắt $SC$ tại $P$ là trung điểm của $SC$
Vậy thiết diện tạo bởi hình chóp với mặt phẳng $\alpha  $ là $MNPQ$ ngoài ra vì :
$MN//CD//PQ\Rightarrow  MNPQ$ là hình thang
$MQ//SA\Rightarrow  MQ\bot (ABCD)\Rightarrow  MQ\bot MN\Rightarrow  MNPQ$ là hình thang vuông
Từ đó ta được :
$S_{MNPQ}=\frac{1}{2} (MN+PQ).MQ$ trong đó :
$MN=\frac{1}{2} (AD+BC)=\frac{3a}{2} $ vì $MN$ là đường trung bình của $ABCD$
$PQ=\frac{1}{2} BC=\frac{a}{2} $ vì $PQ$ là đường trung bình của $\Delta SBC$
$MQ=\frac{1}{2} SA=\frac{a\sqrt{6} }{2} $ vì $MQ$ là đường trung bình của $\Delta SAB$
suy ra :
$S_{MNPQ}=\frac{1}{2} (\frac{3a}{2}+\frac{a}{2}  ).\frac{a\sqrt{6} }{2} =\frac{a^2\sqrt{6} }{2} $