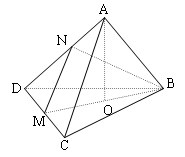
Đề bài: Cho tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO\bot CD$$b.$ Gọi $M$ là trung điểm của $CD$. Tính góc giữa $AC,BM$

Lời giải

$a.$ Ta có ngay kết luận $AO\bot CD$ vì $A.BCD$ là hình chóp tam giác đều
$b.$ Gọi $N$ là trung điểm $AD$ ta có:
$MN//AC\Rightarrow  (AC,BM)=\widehat{BMN} $
Xét $\Delta BMN$ ta có :
$BM=\frac{a\sqrt{3} }{2} $ vì $BM$ là trung tuyến trong $\Delta ABC$ đều
$BN=\frac{a\sqrt{3} }{2} $ vì $BN$ là trung tuyến trong $\Delta ABD$ đều
$MN=\frac{1}{2} AC=\frac{a}{2} $ vì $MN$ là đường trung bình trong $\Delta ACD$
$cos\widehat{BMN}=\frac{MB^2+MN^2-BN^2}{2MB.MN}  =\frac{MN}{2MB}=\frac{\sqrt{3} }{6}  $
Vậy ta được $cos(AC,BM)=\frac{\sqrt{3} }{6} $