Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Hình học không gian

Đề bài: Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình thang, trong đó $\widehat{ABC}=\widehat{BAD}=90^0, BA=BC=a,AD=2a $. Giả sử $SA=a\sqrt{2}$ và $SA$ vuông góc với đáy $ABCD$. Chứng minh $SC \bot CD$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

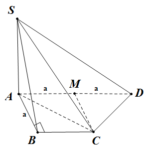
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình thang, trong đó $\widehat{ABC}=\widehat{BAD}=90^0, BA=BC=a,AD=2a $. Giả sử $SA=a\sqrt{2}$ và $SA$ vuông góc với đáy $ABCD$. Chứng minh $SC \bot CD$. Lời giải Gọi $M$ là trung điểm của $AD$, ta có: $MA=MD=a$Do $MA=BC=a; MA//BC \Rightarrow MABC $ là hình vuông.(Kết hợp với $AB=a$ và … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình thang, trong đó $\widehat{ABC}=\widehat{BAD}=90^0, BA=BC=a,AD=2a $. Giả sử $SA=a\sqrt{2}$ và $SA$ vuông góc với đáy $ABCD$. Chứng minh $SC \bot CD$.

Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân với cạnh huyên $AB=a\sqrt{2}$. mặt phẳng $(AA'B)$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AA'=a\sqrt{3}$, góc $\widehat{A'AB}$ nhọn và mặt phẳng $(A'AC)$ tạo với mặt phẳng $ABC)$ góc $60^0$. Tìm thể tích lăng trụ.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân với cạnh huyên $AB=a\sqrt{2}$. mặt phẳng $(AA'B)$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AA'=a\sqrt{3}$, góc $\widehat{A'AB}$ nhọn và mặt phẳng $(A'AC)$ tạo với mặt phẳng $ABC)$ góc $60^0$. Tìm thể tích lăng trụ. Lời giải Cần giải chi tiết (đáp số: … [Đọc thêm...] vềĐề bài: Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân với cạnh huyên $AB=a\sqrt{2}$. mặt phẳng $(AA'B)$ vuông góc với mặt phẳng $(ABC)$. Giả sử $AA'=a\sqrt{3}$, góc $\widehat{A'AB}$ nhọn và mặt phẳng $(A'AC)$ tạo với mặt phẳng $ABC)$ góc $60^0$. Tìm thể tích lăng trụ.

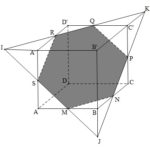
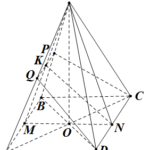
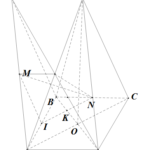
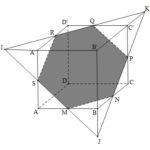
Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$  cắt hình lập phương. 

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$  cắt hình lập phương. 

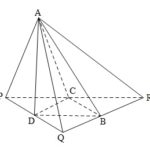
Đề bài: Cho tứ diện $ABCD$ với $AB=CD, AD=BC$ . Trong mặt phẳng $(BCD)$ dựng $\Delta PQR$ sao cho $B, C, D$ lần lượt là trung điểm các cạnh $RQ, RP, PQ$. Chứng minh $AP, AQ, AR$ vuông góc với nhau đôi một.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho tứ diện $ABCD$ với $AB=CD, AD=BC$ . Trong mặt phẳng $(BCD)$ dựng $\Delta PQR$ sao cho $B, C, D$ lần lượt là trung điểm các cạnh $RQ, RP, PQ$. Chứng minh $AP, AQ, AR$ vuông góc với nhau đôi một. Lời giải Từ giả thiết cho $BC//=\frac{1}{2}PQ\Rightarrow AD=BC=PD=DQ$, nên $\Delta APQ$ có đường trung tuyến thuộc cạnh thứ ba bằng nửa cạnh thứ ba $\Rightarrow … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$ với $AB=CD, AD=BC$ . Trong mặt phẳng $(BCD)$ dựng $\Delta PQR$ sao cho $B, C, D$ lần lượt là trung điểm các cạnh $RQ, RP, PQ$. Chứng minh $AP, AQ, AR$ vuông góc với nhau đôi một.

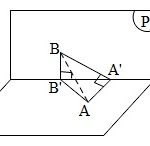
Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau. Lời giải Ta có:Từ $A, B$ theo thứ tự kẻ $AA', BB'$ vuông góc với $d$. Do $P$ vuông góc … [Đọc thêm...] vềĐề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau.

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$. Lời giải Gọi $M,N$ lần lượt là trung điểm $AB,CD. $ Khi đó $\widehat{SNM}=60^0$ là góc giữa … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$, góc giữa hai mặt bên và đáy bằng $60^0$. Dựng thiết diện qua $DC$ và là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng $(SDC),(ABCD)$. Thiết diện chia khối chóp thành hai phần có thể tích $V_1,V_2$. Tìm tỉ số $\frac{V_1}{V_2}$.

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$. Lời giải a. Gọi O là tâm của ABCDI là trung điểm của ABIN giao BO tại K$\begin{cases}IN//AC \\ BD\bot … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho. Lời giải Ta có $A_1O \bot (ABCD)$.Gọi $E$ là trung điểm … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho.

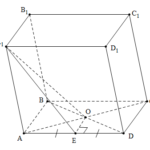
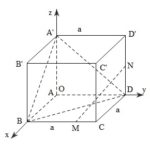
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $a$. Giả sử $M, N$ lần lượt là trung điểm của các cạnh $BC, DD'$a) Chứng minh rằng $MN//mp(A'BD)$B) Tính khoảng cách giữa hai đường thẳng $MN, BD$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $a$. Giả sử $M, N$ lần lượt là trung điểm của các cạnh $BC, DD'$a) Chứng minh rằng $MN//mp(A'BD)$B) Tính khoảng cách giữa hai đường thẳng $MN, BD$ Lời giải a) Chọn hệ trục tọa độ $Oxyz$ như sau:Gốc $O\equiv A$Trục $Ox$ đi qua $AB$Trục $Oy$ đi qua $AD$Trục $Oz$ đi qua $AA'$Khi đó … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $a$. Giả sử $M, N$ lần lượt là trung điểm của các cạnh $BC, DD'$a) Chứng minh rằng $MN//mp(A'BD)$B) Tính khoảng cách giữa hai đường thẳng $MN, BD$

Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$  cắt hình lập phương. 

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$  của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$  với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$  của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$  cắt hình lập phương.