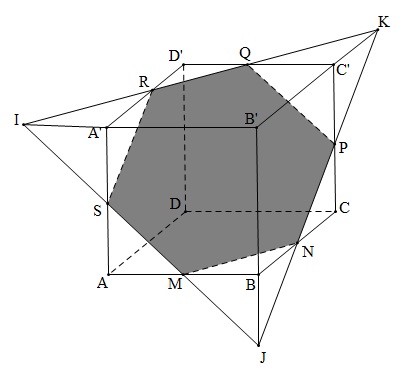
Đề bài: Cho hình lập phương $ABCDA'B'C'D'$ và $R\in A'D', N\in BC, Q\in C'D'$.a) Tìm giao điểm $I, K$ của đường thẳng $RQ$ với mp $(ABB'A')$ mp $(BCC'B')$.b) Tìm giao điểm $P, J$ của đường thẳng $NK$ với mp $(CDD'C')$ và mp $(ABB'A')$c) Tìm giao điểm $S, M$ của đường thẳng $IJ$ với mp $(ADD'A')$ và mp $(ACBD)$.d) Tìm giao tuyến của mp $(NQR)$ với các mặt của hình lập phương .e) Tìm thiết diện do mp $(NQR)$ cắt hình lập phương.

Lời giải
a) $RQ\subset mp A’B’C’D’$, mp $A’B’C’D’$ cắt mp $BCC’B’$ theo giap tuyến $B’C’$, $RQ$ và $B’C’$ cùng thuộc mp $A’B’C’D’$, $RQ$ không song song $B’C’$ nên cắt $B’C’$ tại $K$, $K\in mp BCC’B’$ nên $K$ là giao điểm của $RQ$ với mp $BCC’B’$.
Lập luận tương tự : $I$ là giao điểm của $RQ$ và mp $BCC’B’$.
b) Lập luận tương tự: $P$ là giao điểm của $NK$ và mp $CDD’C’$, $J$ là giao điểm của $NK$ và mp $ABB’A’$.
c) Lâp luận tương tự câu a.
d) Giao tuyến của mp $NQR$ với các mặt của hình lập phương là: $MN, NP, PQ, RQ, RS, SM$.
e) Theo d $\Rightarrow $ thiết diện do mp $NQR$ cắt hình lập phương là $MNPQRS$.

