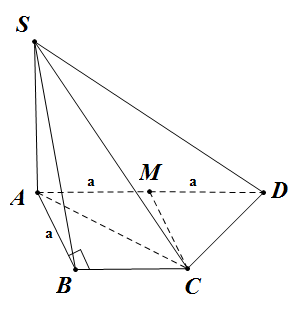
Đề bài: Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình thang, trong đó $\widehat{ABC}=\widehat{BAD}=90^0, BA=BC=a,AD=2a $. Giả sử $SA=a\sqrt{2}$ và $SA$ vuông góc với đáy $ABCD$. Chứng minh $SC \bot CD$.

Lời giải

Gọi $M$ là trung điểm của $AD$, ta có: $MA=MD=a$

Do $MA=BC=a; MA//BC \Rightarrow MABC $ là hình vuông.
(Kết hợp với $AB=a$ và $\widehat{ABC}=\widehat{BAD}=90^0.$)
Từ đó ta có: $MC=a$.
Vì $MA=MD=MC=a$
$\Rightarrow ACD$ là tam giác vuông tại $C$, tứcl à $CA \bot CD$.
Do đó $SC \bot CD$ (định lí ba đường vuông góc).