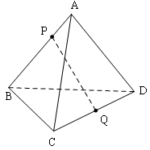
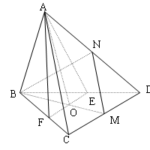
Đề bài: Cho hình tứ diện $ABCD$ trong đó $AB\bot AC, AB\bot BD$. Gọi $P$ và $Q$ là các điểm lần lượt thuộc các đường thẳng $AB$ và $CD$ sao cho $\overrightarrow{PA}=k \overrightarrow{PB}, \overrightarrow{QC}=k \overrightarrow{QD} (k \neq 1)$. Tính góc giữa $AB$ và $PQ.$ Lời giải Ta có $\overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BD}+\overrightarrow{DQ} $, do đó$k \overrightarrow{PQ}=k \overrightarrow{PB}+ […]
Hình học không gian
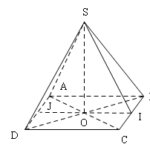
Đề bài: Cho hình chóp $S.ABCD$ có đáy là $ABCD$ là hình thoi tâm $O$, cạnh $a$ góc $\widehat{A}=60^0 $ và có đường cao $SO=a$$a.$ Tính khoảng cách từ $O$ đến $(SBC)$$b.$ Tính khoảng cách giữa hai đường thẳng $AD,SB$
Đề bài: Cho hình chóp $S.ABCD$ có đáy là $ABCD$ là hình thoi tâm $O$, cạnh $a$ góc $\widehat{A}=60^0 $ và có đường cao $SO=a$$a.$ Tính khoảng cách từ $O$ đến $(SBC)$$b.$ Tính khoảng cách giữa hai đường thẳng $AD,SB$ Lời giải $a.$ Hạ $OI$ vuông góc với $BC$ và kéo dài $OI$ cắt $AD$ […]
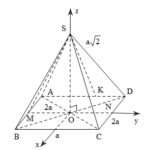
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật $ABCD$ có $AB=2a, BC=a$. Các cạnh bên của hình chóp bằng nhau và bằng $a\sqrt{2} $a) Tính thể tích khối chóp $S.ABCD$b) Gọi $M, N$ lần lượt là trung điểm của các cạnh $AB, CD; K$ là một điểm trên cạnh $AD$ sao cho $AK=\frac{a}{3} $. Tính khoảng cách giữa hai đường thẳng $MN$ và $SK$
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật $ABCD$ có $AB=2a, BC=a$. Các cạnh bên của hình chóp bằng nhau và bằng $a\sqrt{2} $a) Tính thể tích khối chóp $S.ABCD$b) Gọi $M, N$ lần lượt là trung điểm của các cạnh $AB, CD; K$ là một điểm trên cạnh $AD$ sao […]
Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a, AA'=2a, A'C=3a$. Gọi $M$ là trung điểm của $A'C'$ và $I$ là giao điểm của $AM$ và $A'C$. Tính thể tích tứ diện $IABC$.
Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông $ABC$ tại $B$. Giả sử $AB=a, AA'=2a, A'C=3a$. Gọi $M$ là trung điểm của $A'C'$ và $I$ là giao điểm của $AM$ và $A'C$. Tính thể tích tứ diện $IABC$. Lời giải Xét hệ tọa độ $Bxyz$ gốc $B$.Trong hệ trục […]
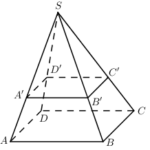
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Một mặt phẳng $(P)$ bất kì không đi qua $S$, cắt các cạnh $SA,SB,SC,SD$ lần lượt tại các điểm $A',B',C',D'$. Chứng minh rằng: $\frac{SA}{SA'}+\frac{SC}{SC'}=\frac{SB}{SB'}+\frac{SD}{SD'}$
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Một mặt phẳng $(P)$ bất kì không đi qua $S$, cắt các cạnh $SA,SB,SC,SD$ lần lượt tại các điểm $A’,B’,C’,D’$. Chứng minh rằng: $\frac{SA}{SA’}+\frac{SC}{SC’}=\frac{SB}{SB’}+\frac{SD}{SD’}$ Lời giải Giả sử $AC$ cắt $BD$ tại $O$ và $A’C’$ cắt $B’D’$ tại $O’$. Đặt: $\overrightarrow {SA}=a.\overrightarrow {SA’},\overrightarrow […]
Đề bài: Từ một điểm $O$ trong không gian ta dựng bốn tia $Ox,Oy,Oz,Ot$.Có tất cả bao nhiêu mặt phẳng được xác định bởi hai trong bốn tia?
Đề bài: Từ một điểm $O$ trong không gian ta dựng bốn tia $Ox,Oy,Oz,Ot$.Có tất cả bao nhiêu mặt phẳng được xác định bởi hai trong bốn tia? Lời giải Ta xét các trường hợp$a.$ Cả bốn tia đồng phẳng : ta có $1$ mặt phẳng$b.$ Ba trong bốn tia đồng phẳng;chẳng hạn ba tia […]
Đề bài: Cho hình tứ diện đều $ABCD$ cạnh $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO$ vuông góc với $CD$$b.$ Gọi $M$ là trung điểm $CD$. Tính góc giữa $AC,BM$
Đề bài: Cho hình tứ diện đều $ABCD$ cạnh $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO$ vuông góc với $CD$$b.$ Gọi $M$ là trung điểm $CD$. Tính góc giữa $AC,BM$ Lời giải $a.$ Qua $O$ dựng đường thẳng song song với $CD$ cắt $BC,BD$ theo thứ tự […]
Đề bài: Cho bốn điểm $O,A,B,C$ không đồng phẳng và bốn điểm $A',B',C',S$ được xác định bởi các hệ thức :$\overrightarrow {OA'}=\overrightarrow {OB}+\overrightarrow {OC} $$\overrightarrow {OB'}=\overrightarrow {OC}+\overrightarrow {OA} $$\overrightarrow {OC'}=\overrightarrow {OA} +\overrightarrow {OB} $$\overrightarrow {OS}=\overrightarrow {OA}+\overrightarrow {OB} +\overrightarrow {OC} $$a.$ Chứng minh các điểm sau đây đồng phẳng- Bốn điểm $A,C',S,B'$- Bốn điểm $C,B',S,A'$- Bốn điểm $B,C',S,A'$$b.$ Xét vị trí tương đối của các cặp mặt phẳng $(OBA'C), (AC'SB')$$(OAC'B), (CB'SA')$$(OAB'C), (BC'SA')$$c.$ Chứng minh hệ thức$\overrightarrow {AS}=\overrightarrow {AB} +\overrightarrow {AC}-2\overrightarrow {AO} $$d.$ Gọi $G$ là giao điểm của $SO$ với $mp(ABC)$.Đặt $\overrightarrow {OG}=k.\overrightarrow {OS} $.Biểu diễn véctơ $\overrightarrow {OG} $ theo các véctơ $\overrightarrow {OA},\overrightarrow {AB},\overrightarrow {AC},k $.Chứng tỏ $G$ là trọng tâm của $\Delta ABC$$e.$ Chứng minh hai mặt phẳng $(ABC),(A'B'C')$ song song
Đề bài: Cho bốn điểm $O,A,B,C$ không đồng phẳng và bốn điểm $A',B',C',S$ được xác định bởi các hệ thức :$\overrightarrow {OA'}=\overrightarrow {OB}+\overrightarrow {OC} $$\overrightarrow {OB'}=\overrightarrow {OC}+\overrightarrow {OA} $$\overrightarrow {OC'}=\overrightarrow {OA} +\overrightarrow {OB} $$\overrightarrow {OS}=\overrightarrow {OA}+\overrightarrow {OB} +\overrightarrow {OC} $$a.$ Chứng minh các điểm sau đây đồng phẳng- Bốn điểm $A,C',S,B'$- Bốn điểm $C,B',S,A'$- Bốn […]
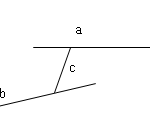
Đề bài: Cho hai đường thẳng $a$ và $b$ chéo nhau. Khi đó hai mệnh đề sau đây có đúng không?1) Không thể tồn tại một đường thẳng cắt cả $a$ và $b$2) Không thể tồn tại hai đường thẳng $c, d$, mỗi đường đều cắt cả $a$ và $b$.
Đề bài: Cho hai đường thẳng $a$ và $b$ chéo nhau. Khi đó hai mệnh đề sau đây có đúng không?1) Không thể tồn tại một đường thẳng cắt cả $a$ và $b$2) Không thể tồn tại hai đường thẳng $c, d$, mỗi đường đều cắt cả $a$ và $b$. Lời giải 1) Sai. Như […]
Đề bài: Cho tứ diện $ABCD.$Một điểm $I$ thuộc đường thẳng $BD$ nhưng không thuộc đoạn thẳng $BD.$Một đường thẳng qua $I$, nằm trong mặt phẳng $(ABD)$ cắt $AB,AD$ theo thứ tự tại các điểm $K,L$ và đường thẳng qua $I$, nằm trong mặt phẳng $(BCD)$ cắt $CB,CD$ theo thứ tự tại $M,N$$a.$ Chứng minh bốn điểm $K,L,M,N$ đồng phẳng$b.$ $BN,DM$ cắt nhau tại $P$ và $BL,DK$ cắt nhau tại $Q;LM,KN$ cắt nhau tại $R$Chứng minh ba điểm $A,P,R$ thẳng hàng và ba điểm $C,R,Q$ cũng thẳng hàng$c.$ $KM,LN$ cắt nhau tại điểm $I$.Chứng minh điểm $J$ thuộc đường thẳng $AC$
Đề bài: Cho tứ diện $ABCD.$Một điểm $I$ thuộc đường thẳng $BD$ nhưng không thuộc đoạn thẳng $BD.$Một đường thẳng qua $I$, nằm trong mặt phẳng $(ABD)$ cắt $AB,AD$ theo thứ tự tại các điểm $K,L$ và đường thẳng qua $I$, nằm trong mặt phẳng $(BCD)$ cắt $CB,CD$ theo thứ tự tại $M,N$$a.$ Chứng minh […]