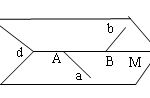
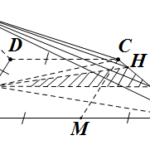
Đề bài: Cho hai đường thẳng $a,b$ chéo nhau và một điểm $M$ không thuộc hai đường thẳng đó. Hãy dựng một đường thẳng qua $M$ cắt cả hai $a,b$ Lời giải $a.$ Phân tích Giả sử dựng được đường thẳng $d$ qua $M$ cắt $a,b$ theo thứ tự tại $A,B$ khi đó :$M,A$ thuộc […]
Hình học không gian
Đề bài: Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, góc giữa hệ mặt phẳng $(A'BC), (ABC)$ bằng $60^0$. Tìm thể tích khối lăng trụ đó.
Đề bài: Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, góc giữa hệ mặt phẳng $(A'BC), (ABC)$ bằng $60^0$. Tìm thể tích khối lăng trụ đó. Lời giải Gọi $M$ là trung điểm $BC$,ta có $AM \bot BC$ $A’M\bot BC$ (định lí ba đường vuông góc) Vậy $\widehat{A’MA}$ là góc tạo bởi hai […]
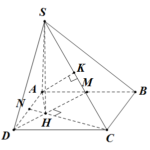
Đề bài: Cho hình chóp $S.ABCD $ đáy là hình vuông $ABCD$ cạnh $a$, mặt bên $SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Goi $M,N,P$ lần lượt là trung điểm $SB,BC,CD$. Tính thể tích tứ diện $CMNP$.
Đề bài: Cho hình chóp $S.ABCD $ đáy là hình vuông $ABCD$ cạnh $a$, mặt bên $SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Goi $M,N,P$ lần lượt là trung điểm $SB,BC,CD$. Tính thể tích tứ diện $CMNP$. Lời giải Gọi $H$ là trung điểm $AD$ thì $SH […]
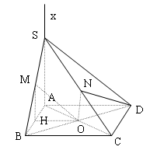
Đề bài: Cho hình vuông $ABCD $ tâm $O;S$ là một điểm di động trên tia $Ax$ vuông góc với mặt phẳng $ABCD$$a.$ Tìm tập hợp hình chiếu vuông góc của $O$ trên đường thẳng $SB$$b.$ Tìm tập hợp chân đường cao vẽ từ đỉnh $D$ trong $\Delta SDC$
Đề bài: Cho hình vuông $ABCD $ tâm $O;S$ là một điểm di động trên tia $Ax$ vuông góc với mặt phẳng $ABCD$$a.$ Tìm tập hợp hình chiếu vuông góc của $O$ trên đường thẳng $SB$$b.$ Tìm tập hợp chân đường cao vẽ từ đỉnh $D$ trong $\Delta SDC$ Lời giải $a.$ Nhận thấy đường […]
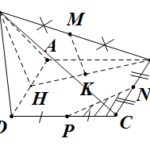
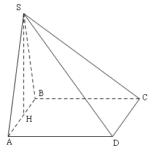
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Gọi $M,N$ lần lượt là trung điểm của cạnh $AB,AD;H$ là giao điểm của $CN,DM$. Biết $SH$ vuông góc với mặt phẳng $(ABCD)$ và $SH=a\sqrt{3}$. Tìm khoảng cách giữa hai đường thẳng $DM,SC$ theo $a$.
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Gọi $M,N$ lần lượt là trung điểm của cạnh $AB,AD;H$ là giao điểm của $CN,DM$. Biết $SH$ vuông góc với mặt phẳng $(ABCD)$ và $SH=a\sqrt{3}$. Tìm khoảng cách giữa hai đường thẳng $DM,SC$ theo $a$. Lời giải Do $ABCD$ là hình vuông […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A, D; AB=2AD=2a; CD=a$, góc giữa hai mặt phẳng $(SBC)$ và $(ABCD)$ bằng $60^0$ . Gọi $I$ là trung điểm của cạnh $AD$. Biết mặt phẳng $(SBI)$ và $(SCI)$cùng vuông góc với mặt phẳng $ABCD$. Tính thể tích khối chóp $S.ABCD$.
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A, D; AB=2AD=2a; CD=a$, góc giữa hai mặt phẳng $(SBC)$ và $(ABCD)$ bằng $60^0$ . Gọi $I$ là trung điểm của cạnh $AD$. Biết mặt phẳng $(SBI)$ và $(SCI)$cùng vuông góc với mặt phẳng $ABCD$. Tính thể tích khối chóp $S.ABCD$. Lời […]
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng $60^{*}$. Tính thể tích khối chóp S.ABCD theo a.
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng $60^{*}$. Tính thể tích khối chóp S.ABCD theo a. Lời giải Độc giả tự vẽ hình.Giả sử $AC\cap BD\equiv I.$Ta có:$\left\{ \begin{array}{l} […]
Đề bài: Cho $S.ABCD$ có đáy là hình chữ nhất với $AB=a, AD=2a$. Cạnh $SA$ vuông góc với đáy, còn cạnh $SB$ tạo với mặt phẳng đáy góc $60^0$. Trên cạnh $SA$ lấy điểm $M$ sao cho $AM=\frac{a\sqrt{3}}{3}$. mặt phẳng $(BCM)$ cắt $SD$ tại điểm $N $ . Tính thể tích khối chóp $S.BCNM$.
Đề bài: Cho $S.ABCD$ có đáy là hình chữ nhất với $AB=a, AD=2a$. Cạnh $SA$ vuông góc với đáy, còn cạnh $SB$ tạo với mặt phẳng đáy góc $60^0$. Trên cạnh $SA$ lấy điểm $M$ sao cho $AM=\frac{a\sqrt{3}}{3}$. mặt phẳng $(BCM)$ cắt $SD$ tại điểm $N $ . Tính thể tích khối chóp $S.BCNM$. Lời […]
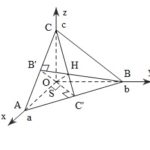
Đề bài: Cho hình chóp $S.ABC$ có ba cạnh $SA, SB, SC$ vuông góc với nhau từng đôi một và $SA=a, SB=b, SC=c$a) Tính thể tích khối chóp $S.ABC$. Chứng minh rằng hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABC)$ là trực tâm tam giác $ABC$b) Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp $S.ABC$
Đề bài: Cho hình chóp $S.ABC$ có ba cạnh $SA, SB, SC$ vuông góc với nhau từng đôi một và $SA=a, SB=b, SC=c$a) Tính thể tích khối chóp $S.ABC$. Chứng minh rằng hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABC)$ là trực tâm tam giác $ABC$b) Tìm tâm và bán kính mặt […]
Đề bài: cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, tam giác $SAB$ đều và $mp(ABCD)$ vuông góc với $mp(SAB)$$a.$ Chứng minh rằng $mp(SAD)\bot mp(SAB)$$b.$ Tính góc giữa $AB$ và $SC$
Đề bài: cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, tam giác $SAB$ đều và $mp(ABCD)$ vuông góc với $mp(SAB)$$a.$ Chứng minh rằng $mp(SAD)\bot mp(SAB)$$b.$ Tính góc giữa $AB$ và $SC$ Lời giải $a.$ Vì $mp(SAB)\bot mp(ABCD)$ và $AD\bot AB,AD\bot (SAB)$ từ đó $(SAD)\bot (SAB)$$b.$ Vì $AB//CD$ nên góc giữa $AB$ và $SC$ […]