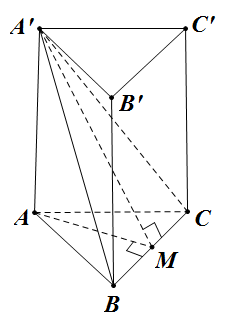
Đề bài: Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, góc giữa hệ mặt phẳng $(A'BC), (ABC)$ bằng $60^0$. Tìm thể tích khối lăng trụ đó.

Lời giải

Gọi $M$ là trung điểm $BC$,ta có $AM \bot BC$    
$A’M\bot BC$ (định lí ba đường vuông góc)

Vậy $\widehat{A’MA}$ là góc tạo bởi hai mặt phẳng $(A’BC), (ABC)$ và $\widehat{A’MA}=60^0$
Từ đó : $A’A=AM \tan \widehat{A’MA}=\frac{a\sqrt{3}}{2}. \tan 60^0=\frac{3a}{2}$
$\Rightarrow V_{ABC.A’B’C’}=AA’.S_{ABC}= \frac{3a}{2}.\frac{a^2\sqrt{3}}{4}=\frac{3a^3\sqrt{3}}{8}$ (đvtt)