Hình học không gian

Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a$, có $SA=h$ và vuông góc với mặt phẳng $(ABCD)$. Dựng và tính độ dài đoạn vuông góc chung của :1) $SB$ và $CD$.2) $SC$ và $BD$.

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

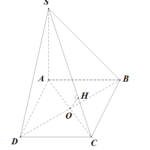
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a$, có $SA=h$ và vuông góc với mặt phẳng $(ABCD)$. Dựng và tính độ dài đoạn vuông góc chung của :1) $SB$ và $CD$.2) $SC$ và $BD$. Lời giải a.$AB\bot BC, SA\bot BC\Rightarrow BC\bot (SAB)\Rightarrow BC\bot SB$ mà $BC\bot CD\Rightarrow $ BC là đoạn vuông góc chung của SB và CD; $BC=a$b. O là tâm … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a$, có $SA=h$ và vuông góc với mặt phẳng $(ABCD)$. Dựng và tính độ dài đoạn vuông góc chung của :1) $SB$ và $CD$.2) $SC$ và $BD$.

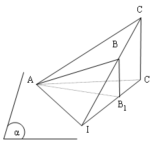
Đề bài: Cho $\Delta ABC$ có đỉnh $A$ nằm trong mặt phẳng $(\alpha) $ hai đỉnh $B,C$ có hình chiếu xuống $(\alpha) $ lần lượt là $B_1,C_1$ sao cho $\Delta AB_1C_1$ là tam giác đều cạnh $a$. Giả sử $CC_1=a$ và $BB_1=\frac{a}{2} $.Gọi $I$ là giao điểm của $BC,B_1C_1$$a.$ Chứng minh rằng $IA\bot AC$$b.$ Tính diện tích $\Delta ABC$ rồi suy ra giá trị của góc $\varphi$ giữa hai mặt phẳng $(\alpha) $ và $(ABC)$

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho $\Delta ABC$ có đỉnh $A$ nằm trong mặt phẳng $(\alpha) $ hai đỉnh $B,C$ có hình chiếu xuống $(\alpha) $ lần lượt là $B_1,C_1$ sao cho $\Delta AB_1C_1$ là tam giác đều cạnh $a$. Giả sử $CC_1=a$ và $BB_1=\frac{a}{2} $.Gọi $I$ là giao điểm của $BC,B_1C_1$$a.$ Chứng minh rằng $IA\bot AC$$b.$ Tính diện tích $\Delta ABC$ rồi suy ra giá trị của góc $\varphi$ giữa hai mặt … [Đọc thêm...] vềĐề bài: Cho $\Delta ABC$ có đỉnh $A$ nằm trong mặt phẳng $(\alpha) $ hai đỉnh $B,C$ có hình chiếu xuống $(\alpha) $ lần lượt là $B_1,C_1$ sao cho $\Delta AB_1C_1$ là tam giác đều cạnh $a$. Giả sử $CC_1=a$ và $BB_1=\frac{a}{2} $.Gọi $I$ là giao điểm của $BC,B_1C_1$$a.$ Chứng minh rằng $IA\bot AC$$b.$ Tính diện tích $\Delta ABC$ rồi suy ra giá trị của góc $\varphi$ giữa hai mặt phẳng $(\alpha) $ và $(ABC)$

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$.

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Vectơ trong không gian

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$. Lời giải Đặt $\overrightarrow{AA'}=\overrightarrow{a}, … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$.

Đề bài: Cho tứ diện $OABC$ vuông tại $O$ biết $AB=BC=5;CA=3\sqrt{2} $$a.$ Tính $OA,OB,OC$$b.$ Kẻ $OH\bot (ABC)$. Tính $OH$ và diện tích các tam giác $OAB,OAC,OBC,ABC$

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Cho tứ diện $OABC$ vuông tại $O$ biết $AB=BC=5;CA=3\sqrt{2} $$a.$ Tính $OA,OB,OC$$b.$ Kẻ $OH\bot (ABC)$. Tính $OH$ và diện tích các tam giác $OAB,OAC,OBC,ABC$ Lời giải (bạn đọc vẽ hình để theo dõi )$a,$ Vì $AB=BC=5$ nên sử dụng định lí pytago trong các tam giác vuông $AOB,COB$ ta suy ra : $OA=OC$Đặt $OA=OC=a;OB=b$ ta có :$\begin{cases}a^2+b^2=5^2=25 \\ … [Đọc thêm...] vềĐề bài: Cho tứ diện $OABC$ vuông tại $O$ biết $AB=BC=5;CA=3\sqrt{2} $$a.$ Tính $OA,OB,OC$$b.$ Kẻ $OH\bot (ABC)$. Tính $OH$ và diện tích các tam giác $OAB,OAC,OBC,ABC$

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ mà khoảng cách từ điểm $A$ đến mặt phẳng $(SBC)$ bằng $2a$. Với giá trị nào của $\alpha$, với $\alpha $ là góc giữa mặt bên và đáy của hình chóp, thì thể tích khối chóp là nhỏ nhất. Tính giá trị nhỏ nhất đó.

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Thể tích khối đa diện

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ mà khoảng cách từ điểm $A$ đến mặt phẳng $(SBC)$ bằng $2a$. Với giá trị nào của $\alpha$, với $\alpha $ là góc giữa mặt bên và đáy của hình chóp, thì thể tích khối chóp là nhỏ nhất. Tính giá trị nhỏ nhất đó. Lời giải Goi $M,N$ lần lượt là trung điểm $AD,BC$. Ta có $\widehat{SNM}= \alpha$.Do $DA//BC \Rightarrow AD// (SBC) … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ mà khoảng cách từ điểm $A$ đến mặt phẳng $(SBC)$ bằng $2a$. Với giá trị nào của $\alpha$, với $\alpha $ là góc giữa mặt bên và đáy của hình chóp, thì thể tích khối chóp là nhỏ nhất. Tính giá trị nhỏ nhất đó.

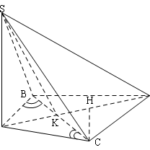
Đề bài: Cho tam giác $ABC$ cạnh $a$, đường cao $AH$. Trên tia $AH$ ta lấy một điểm $I$ biết $AI=\frac{1}{3} AH$. Trên đường thẳng $\Delta $ vuông góc với mặt phẳng $(ABC)$ tại điểm $I$, lấy một điểm $S, IS=a$$a.$ Chứng minh $SB\bot BA,SC\bot CA$$b.$ Tính diện tích các mặt bên của hình chóp $SABC$

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Cho tam giác $ABC$ cạnh $a$, đường cao $AH$. Trên tia $AH$ ta lấy một điểm $I$ biết $AI=\frac{1}{3} AH$. Trên đường thẳng $\Delta $ vuông góc với mặt phẳng $(ABC)$ tại điểm $I$, lấy một điểm $S, IS=a$$a.$ Chứng minh $SB\bot BA,SC\bot CA$$b.$ Tính diện tích các mặt bên của hình chóp $SABC$ Lời giải $a.$ Để thấy $H$ và $I$ đối xứng với nhau qua $BC$ suy ra … [Đọc thêm...] vềĐề bài: Cho tam giác $ABC$ cạnh $a$, đường cao $AH$. Trên tia $AH$ ta lấy một điểm $I$ biết $AI=\frac{1}{3} AH$. Trên đường thẳng $\Delta $ vuông góc với mặt phẳng $(ABC)$ tại điểm $I$, lấy một điểm $S, IS=a$$a.$ Chứng minh $SB\bot BA,SC\bot CA$$b.$ Tính diện tích các mặt bên của hình chóp $SABC$

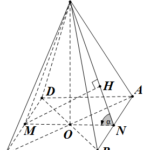
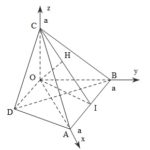
Đề bài: Trên 3 cạnh của một tam diện vuông đỉnh $O$ ta lấy $OA=OB=OC=a$a) Chứng minh rằng tam giác $ABC$ đều và tính diện tích của nób) Tính độ dài đừng cao hạ từ $O$ xuống mặt phẳng $(ABC)$. Gọi $D$ là điểm đối xứng của $H$ qua $O$. Chứng minh rằng $ABCD$ là tứ diện đều

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Quan he vuong goc

Đề bài: Trên 3 cạnh của một tam diện vuông đỉnh $O$ ta lấy $OA=OB=OC=a$a) Chứng minh rằng tam giác $ABC$ đều và tính diện tích của nób) Tính độ dài đừng cao hạ từ $O$ xuống mặt phẳng $(ABC)$. Gọi $D$ là điểm đối xứng của $H$ qua $O$. Chứng minh rằng $ABCD$ là tứ diện đều Lời giải a) Chọn hệ trục tọa độ $Oxyz$ như sau:- Gốc $O$ là đỉnh tam diện- Trục $Ox$ đi qua … [Đọc thêm...] vềĐề bài: Trên 3 cạnh của một tam diện vuông đỉnh $O$ ta lấy $OA=OB=OC=a$a) Chứng minh rằng tam giác $ABC$ đều và tính diện tích của nób) Tính độ dài đừng cao hạ từ $O$ xuống mặt phẳng $(ABC)$. Gọi $D$ là điểm đối xứng của $H$ qua $O$. Chứng minh rằng $ABCD$ là tứ diện đều

Đề bài: Cho một khối tứ diện đều, hãy chứng minh rằng:a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.b) Các trung điểm của các cạnh của nó là các đỉnh của một khối $8$ mặt đều.

Ngày 20/10/2020 Thuộc chủ đề:Hình học không gian Tag với:Hình học không gian

Đề bài: Cho một khối tứ diện đều, hãy chứng minh rằng:a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.b) Các trung điểm của các cạnh của nó là các đỉnh của một khối $8$ mặt đều. Lời giải a) Với tứ diện đều $ABCD$, gọi $G_1,G_2,G_3,G_4,G$ theo thứ tự là trọng tâm của các tam giác $\Delta ABC, \Delta ABD, \Delta ACD, \Delta BCD$ và tứ diện … [Đọc thêm...] vềĐề bài: Cho một khối tứ diện đều, hãy chứng minh rằng:a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.b) Các trung điểm của các cạnh của nó là các đỉnh của một khối $8$ mặt đều.