
Lời giải

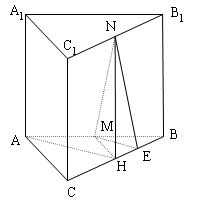
$a.$ Gọi $H$ là trung điểm của $BC$ ta có :
$NH//BB_1\Rightarrow NH\bot (ABC)$
suy ra $MH$ là hình chiếu vuông góc của $MN$ trên $(ABC)$ do đó :
$(MN,(ABC))=\widehat{NMH}=\alpha $
Ngoài ra :
$\begin{cases} AH\bot BC\\AH\bot BB_1\end{cases} \Rightarrow AH\bot (BCC_1B_1)$
Gọi $E$ là trung điểm $BH$ suy ra :
$ME//AH\Rightarrow ME\bot (BCC_1B_1)$
suy ra $NE$ là hình chiếu vuông góc của $MN$ trên $BCC_1B_1$ do đó :
$(MN,(BCC_1B_1))=\widehat{MNE}=\beta $
Trong $\Delta MNH$ vuông tại $H$ ta có :
$MH=MNcos\widehat{NMH}=a.cos\alpha $
$NH=MN.sin\widehat{NMH}=a.sin\alpha \Rightarrow AA_1=a.sin\alpha $
Trong $\Delta ABC$ cân tại $A$ vì $MH$ là đường trung bình nên :
$AB=AC=2MH=2a.cos\alpha $
$BC=\sqrt{AB^2+AC^2}=2\sqrt{2}a.cos\alpha $
$AH=\frac{1}{2} BC=\sqrt{2}a.cos\alpha $
$b.$ Trong $\Delta MNE$ vuông $E$ ta có :
$sin\beta =\frac{BE}{MN} =\frac{\frac{1}{2}AH }{MN} =\frac{\frac{1}{2}\sqrt{2}.cos\alpha }{a} =\frac{cos\alpha }{\sqrt{2} } \Leftrightarrow cos\alpha =\sqrt{2}sin\beta $
