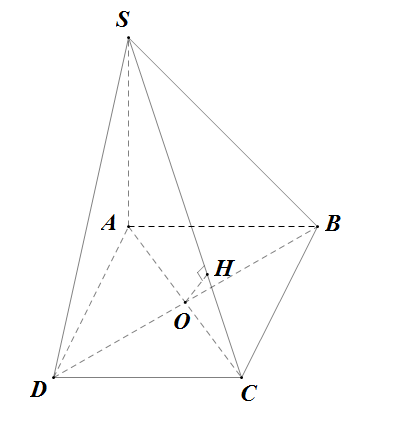
Đề bài: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a$, có $SA=h$ và vuông góc với mặt phẳng $(ABCD)$. Dựng và tính độ dài đoạn vuông góc chung của :1)  $SB$ và $CD$.2)  $SC$ và $BD$.

Lời giải

a.$AB\bot BC, SA\bot BC\Rightarrow BC\bot (SAB)\Rightarrow BC\bot SB$    mà $BC\bot CD\Rightarrow $    BC là đoạn vuông góc chung của SB và CD; $BC=a$
b. O là tâm của ABCD
Trong (SAC) dựng    $OH\bot SC$
$BD\bot AC; BD\bot SA\Rightarrow BD\bot (SAC)\Rightarrow BD\bot OH\Rightarrow $    OH là đoạn vuông góc chung của SC và BD
$\Delta OHC\sim \Delta CAS\Leftrightarrow \frac{OH}{CA}=\frac{OC}{CS}\Leftrightarrow OH=\frac{CA.OC}{CS}=\frac{a\sqrt2.\frac{a\sqrt2}{2}}{\sqrt{2a^2+h^2}}=\frac{a^2}{
\sqrt{2a^2+h^2} }$