Đề bài: Trên 3 cạnh của một tam diện vuông đỉnh $O$ ta lấy $OA=OB=OC=a$a) Chứng minh rằng tam giác $ABC$ đều và tính diện tích của nób) Tính độ dài đừng cao hạ từ $O$ xuống mặt phẳng $(ABC)$. Gọi $D$ là điểm đối xứng của $H$ qua $O$. Chứng minh rằng $ABCD$ là tứ diện đều

Lời giải

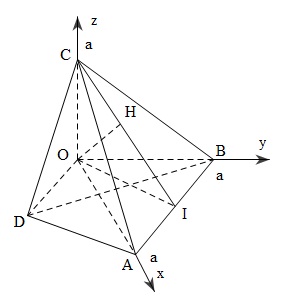
a) Chọn hệ trục tọa độ $Oxyz$ như sau:
– Gốc $O$ là đỉnh tam diện
– Trục $Ox$ đi qua $OA$
– Trục $Oy$ đi qua $OB$
– Trục $Oz$ đi qua $OC$

Khi đó $A(0;0;0), B(0;a;0), C(0;0;a)$
$\Rightarrow  \overrightarrow{AB}=(-a;a;0)\Rightarrow  AB=\sqrt{2a^2}=a\sqrt{2}   $
      $\overrightarrow{AC}=(-a;0;a)\Rightarrow  AC=\sqrt{2a^2}=a\sqrt{2}   $
      $\overrightarrow{BC}=(0;-a;a)\Rightarrow  BC=\sqrt{2a^2}a\sqrt{2}   $
$\Rightarrow  AB=AC=BC\Rightarrow  \Delta ABC$ đều
$\Rightarrow  S_{ABC}=AB^2 \frac{\sqrt{3} }{4}  =2a^2\frac{\sqrt{3} }{4} =\frac{a^2\sqrt{3} }{2} $

b) Ta có: $(ABC):\frac{x}{a}+\frac{y}{a}+\frac{z}{a} =1\Leftrightarrow  x+y+z-a=0  $
$\Rightarrow  OH=d(O,(ABC))=\frac{|-a|}{\sqrt{3} } =\frac{a}{\sqrt{3} }=\frac{a\sqrt{3} }{3}  $
Gọi $d$ là đường thẳng qua $O$ và vuông góc với $(ABC)$
$\Rightarrow  \overrightarrow{u}_d =\overrightarrow{n}_{(ABC)}=(1;1;1) \Rightarrow  d:\left\{ \begin{array}{l} x=t\\ y=t\\z=t \end{array} \right. (t\in R)$
Thay vào phương trình của $(ABC):t+t+t-a=0\Leftrightarrow  t=\frac{a}{3} $
$\Rightarrow  $ Giao điểm của $d$ và $(ABC)$là: $H(\frac{a}{3};\frac{a}{3};\frac{a}{3} )$

$D$ đối xứng với $H$ qua $O\Rightarrow  D(-\frac{a}{3};-\frac{a}{3};-\frac{a}{3})$
Ta có: $\overrightarrow{DA}=(\frac{4a}{3};\frac{a}{3};\frac{a}{3} ) \Rightarrow  DA=\sqrt{2a^2}=a\sqrt{2}  $
$\overrightarrow{DB}=(\frac{a}{3};\frac{4a}{3};\frac{a}{3}) \Rightarrow  DB=\sqrt{2a^2}=a\sqrt{2}  $
$\overrightarrow{DC}=(\frac{a}{3};\frac{a}{3};\frac{4a}{3}) \Rightarrow  DC=\sqrt{2a^2}=a\sqrt{2}  $
$\Rightarrow  DA=DB=DC=AB=AC=BC=a\sqrt{2} $
Vậy $ABCD$ là tứ diện đều