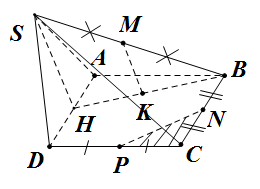
Đề bài: Cho hình chóp $S.ABCD $ đáy là hình vuông $ABCD$ cạnh $a$, mặt bên $SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Goi $M,N,P$ lần lượt là trung điểm $SB,BC,CD$. Tính thể tích tứ diện $CMNP$.

Lời giải

Gọi $H$ là trung điểm $AD$ thì $SH \bot AD$.
Do $(SAD)\bot (ABCD)$ nên suy ra:
  $SH \bot (ABCD); SH =\frac{a\sqrt{3}}{2}$ ( vì $ABC$ là tam giác đều cạnh $a$).
Kẻ $MK // SH (K \in HB)$

$\Rightarrow MK \bot (ABCD)$ và $MK=\frac{SH}{2}=\frac{a\sqrt{3}}{4}$.
Vậy : $V_{M.CNP}=\frac{1}{3}S_{CNP}.MK=\frac{1}{3}.\frac{a^2}{8}.\frac{a\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{96}$ (đvtt).