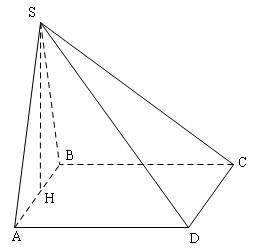
Đề bài: cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, tam giác $SAB$ đều và $mp(ABCD)$ vuông góc với $mp(SAB)$$a.$ Chứng minh rằng $mp(SAD)\bot mp(SAB)$$b.$ Tính góc giữa $AB$ và $SC$

Lời giải

$a.$ Vì $mp(SAB)\bot mp(ABCD)$ và $AD\bot AB,AD\bot (SAB)$ từ đó $(SAD)\bot (SAB)$
$b.$ Vì $AB//CD$ nên góc giữa $AB$ và $SC$ bằng góc giữa $CD$ và $SC$.Ta cần tính góc $\widehat{SCD} $
Gọi $a$ là cạnh hình vuông $ABCD$ ta có : $SA=a$ nên $SC=a\sqrt{2},SD=a\sqrt{2},CD=a $
Vậy $SD^2=CS^2+CD^2-2CS.CDcos\widehat{SCD} $ hay $2a^2=2a^2+a^2-2.a^2\sqrt{2}cos\widehat{SCD} $
suy ra $cos\widehat{SCD}=\frac{1}{2\sqrt{2} } $
Vậy góc giữa $SC$ và $AB$ bằng $\alpha$ với $cos\alpha=\frac{1}{2\sqrt{2} } $
