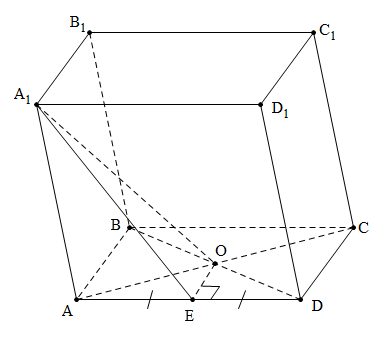
Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$là hình chữ nhật với $AB =a; AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ trên $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1) , (ABCD)$ tạo với nhau một góc $60^0$.Tìm thể tích lăng trụ đã cho.

Lời giải

Ta có $A_1O \bot (ABCD)$.
Gọi $E$ là trung điểm của $AD$, ta có $OE \bot AD$

$\Rightarrow A_1E \bot AD$ (định lí ba đường vuông góc)
Vì $(ADD_1A_1) \cap (ABCD)=AD$
$\Rightarrow \widehat{A_1EO}$ là góc giữa hai mặt phẳng này
$\Rightarrow \widehat{A_1EO}=60^0$
Ta có: $A_1O=OE \tan \widehat{A_1EO}=\frac{a}{2}\sqrt{3}$
$\Rightarrow  V_{ABCD.A_1B_1C_1D_1}=S_{ABCD}.A_1O=a.a\sqrt{3}.\frac{a\sqrt{3}}{2}=\frac{3a^2}{2} $ (đvtt).