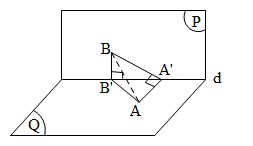
Đề bài: Cho hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau, gọi $d$ là giao tuyến của chúng. Cho $2$ điểm $A\in (Q), B\in (P)$ thỏa mãn khoảng cách từ $B$ đến $(Q)$ bằng khoảng cách từ $A$ đến $(P)$. Chứng minh góc tạo bởi $AB$ với mặt phẳng $(P)$ và mặt phẳng $(Q)$ bằng nhau.

Lời giải
Ta có:
Từ $A, B$ theo thứ tự kẻ $AA’, BB’$ vuông góc với $d$. Do $P$ vuông góc với $Q$ nên $AA’$ vuông góc với $P$ và $BB’$ vuông góc với $Q$ nên $AA’$ là khoảng cách từ $B$ đển $Q$. Theo giả thiết $AA’=BB’$. Mặt khác hình chiếu của $AB$ trên $P$ là $A’B$, hình chiếu $AB$ trên Q là $AB’$. Vậy góc tạo bởi $AB$ và mặt $P$ là $\widehat{ABA”}$, góc tạo bởi $AB$ trên mặt $Q$ là $\widehat{BAB’}$.
Dễ dàng có $\sin \widehat{ABA’}=\frac{AA’}{AB}, \sin\widehat{BAB’}= \frac{BB’}{AB}$.
Mà $AA’$=$BB’\Rightarrow \sin \widehat{ABA’}=\sin \widehat{BAB’}$ ($\widehat{ABA’}

