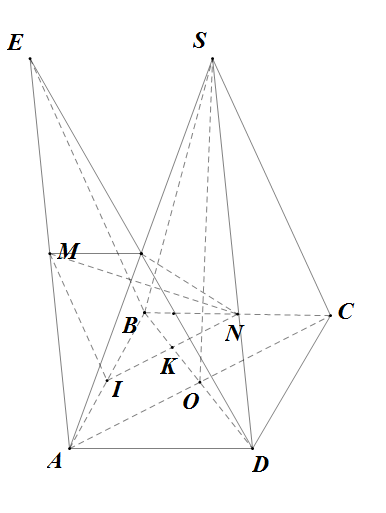
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

Lời giải

a. Gọi O là tâm của ABCD
I là trung điểm của AB
IN giao BO tại K
$\begin{cases}IN//AC \\ BD\bot AC\end{cases}\Rightarrow BD\bot IN(1)$
$\begin{cases}MI//BE \\BE//SC \\ BD\bot SC\end{cases}\Rightarrow BD\bot MI (2)$
(1)  và (2) $\Rightarrow BD\bot (MNI)\Rightarrow BD\bot MN$
b. $AC//IN\Rightarrow AC//(MIN)\Rightarrow d(AC,MN)=d(AC,(MNI))=d(O,(MNI))$
$OK\bot (MIN)\Rightarrow d(O,(MNI))=OK=\frac{a\sqrt2}2=d(MN,AC)$