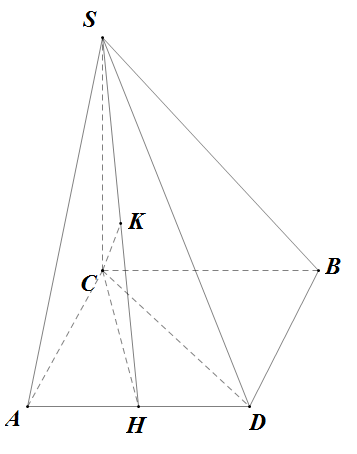
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$.

Lời giải

Trong (ABC) dựng hình bình hành ADBC
Trong (ADC) dựng CH$\bot$AD
Trong (SCH) dựng CK$\bot$SH
AD$\bot$CH; AD$\bot$SC$\Rightarrow $AD$\bot$ (SCH) $\Rightarrow$ AD $\bot$ CK mà CK$\bot$SH$\Rightarrow $CK$\bot$(SAD)
AD//BC$\Rightarrow $BC//(SAD)$\Leftrightarrow $d(SA,BC)=d(BC,(SAD))=d(C,(SAD))=CK
$CH=7a.\frac{\sqrt3}2$
Trong $\Delta$  vuông SCH có:$
\frac1{CK^2} =\frac1{SC^2}+\frac1{CH^2}=\frac1{(7a)^2}+\frac1{(\frac{7a\sqrt3}{2})^2}=\frac1{21a^2}\Rightarrow CK=a\sqrt{21}$