
Lời giải

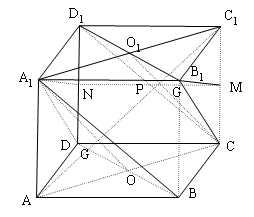
$a.$ Gọi $O,O_1$ theo thứ tự là tâm của các hình bình hành $ABCD,A_1B_1C_1D_1$ ta có :
$\begin{cases}A_1O//CO_1\\BD//B_1D_1 \end{cases} \Rightarrow (BDA_1)//(B_1D_1C)$
$b.$ Vì $AC_1,AO,CO_1$ cùng nằm trong mặt phẳng $(ACC_1A_1)$ nên gọi :
$G=AC_1\cap A_1O$ và $G_1=AC_1\cap CO_1$
– Trong $\Delta A_1BD$ điểm $G$ thuộc trung tuyến $A_1O$ và vì $AO//A_1C_1$ nên :
$\frac{GO}{GA_1}=\frac{AO}{A_1C_1}=\frac{1}{2} $
do đó $G$ là trọng tâm $\Delta A_1BD$
– Chứng minh tương tự $G_1$ là trọng tâm $\Delta CB_1D_1$
Nhận xét rằng $OG,O_1G_1$ theo thứ tự là đường trung bình của $\Delta ACG_1, A_1C_1G$ nên ta có :
$AG=GG_1=G_1C_1$
tức là $GG_1$ chia đoạn $AC_1$ làm $3$ phần bằng nhau.
$c.$ Kéo dài $B_1G_1$ cắt $CD_1$ tại $P$ ta có $P$ là trung điểm của $CD_1$ vì $G_1$ là trọng tâm của $\Delta CB_1D_1$
Ta có:
$\begin{cases} A_1B_1\in (A_1B_1G_1)\end{cases} và C_1D_1\in (CDD_1C_1)\\alpha_1B_1//C_1D_1\\(A_1B_1G_1)\cap (CDD_1C_1)=Px\Rightarrow Px//A_1B_1//C_1D_1$
giả sử $Px$ theo thứ tự cắt $CC_1,DD_1$ tại $M,N$
khi đó ta nhận được thiết diện $A_1B_1MN$ là hình bình hành
$d.$ Ta lần lượt có :
– Trong $(A_1B_1CD)$ giả sử : $A_1K$\cap DC=I
– Nối $IO$ cắt $BC,AD$ theo thứ tự tại $E, F$
– Nối $KE$ cắt $B_1C_1$ tại $H$
Nối $A_1F,A_1H$ nhận được thiết diện $A_1FEH$ là hình bình hành.
