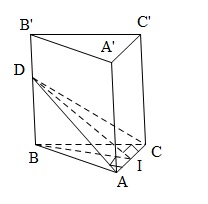
Đề bài: Đáy của lăng trụ đứng $ABC.A'B'C'$ là một tam giác cân đỉnh $B$, $BA=BC=7$, $AC=2$. Qua $AC$ ta vẽ một mặt phẳng tạo với đáy dưới một góc $30^0$, cắt cạnh bên tại $D$. Tìm diện tích thiết diện và độ dài $BD$.

Lời giải

Ta có:
Kẻ $BI$ vuông góc với $AC$ thì $I$ là trung điểm của $AC$. $BI$ là hình chiếu của $DI$ trên đáy nên $DI$ vuông góc với $AC$ theo định lí ba đường vuông góc $\Rightarrow \widehat{DIB}$ là góc phẳng tạo bởi thiết diện và đáy $\Rightarrow \widehat{DIB}=30^0$.
Tam giác vuông  $DIB$ cho $BD=BI\tan 30^0$
Áp dụng định lí Pitago vào tam giác vuông $BAI$ cho:
$BI^2=AB^2-AI^2=48\Rightarrow BI=4\sqrt{3}$. Vậy $BD=4\sqrt{3}.\frac{1}{\sqrt{3}}=4.$ 
$dt\Delta ABC=\frac{1}{2}AC.BI=4\sqrt{3}, dt \Delta ACD=\frac{dt \Delta ABC}{\cos 30^0}=8.$