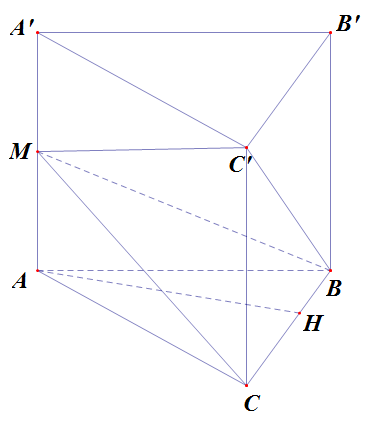
Đề bài: Cho hình lăng trụ đứng $ABC.A'B'C'$. Gọi $M$ là trung điểm của $AA'$. Chứng minh rằng thiết diện $C'MB$ chia lăng trụ thành hai phần tương đương.

Lời giải

Trong (ABC) dựng AH $\bot$ BC
$V_{M.ABC}=\frac13MA.S_{ABC}=\frac16V_{ABC.A’B’C’}$
$V_{M.CBC’}=\frac13d(M,(CBC’)).S_{CBC’}=
\frac13AH.S_{CBC’} = \frac13V_{ABC.A’B’C’} $
$\Rightarrow V_{ABCMC’}=V_{MABC}+V_{C’MBC}=\frac12V_{ABCA’B’C’}$