Đề bài: Một lăng trụ tứ giác đều có cạnh đáy $a$, đường chéo của lăng trụ tạo với  cạnh bên và với đường chéo đáy hai góc có tổng bằng $135^0$. Xác định đường cao lăng trụ.

Lời giải

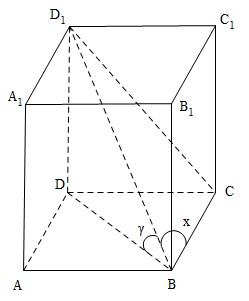
Kí hiệu góc giữa  đường chéo $D_1B$ và đường chéo đáy $DB$ là $y$ và góc giữa $D_1B$ và $BC$ là $x$, theo giả thiết $x+y=135^0$
Ta có $\left. {\begin{array}{*{20}{c}}
BC=\cos x.BD_1=a\\
BD=\cos y.BD_1=a\sqrt{2}
\end{array}} \right\}    (1)$
Do $(1)$ ta có: $\frac{\cos x}{\cos y}=\frac{1}{\sqrt{2}} \Leftrightarrow \frac{\cos y}{\cos (135^0-y)}=\sqrt{2}$
Giải phương trình: $\cos y=\sqrt{2}\cos (135^0-y)$
                  $\cos (135^0-y)=-\cos(45^0+y)=-\frac{\sqrt{2}}{2}(\cos y-\sin y)$
Nên $-\cos y+\sin y=\cos y \Leftrightarrow \sin y=2\cos y \Rightarrow \tan y=2$
Đường cao $DD_1=BD\tan y=a\sqrt{2}\tan y=2a\sqrt{2}$