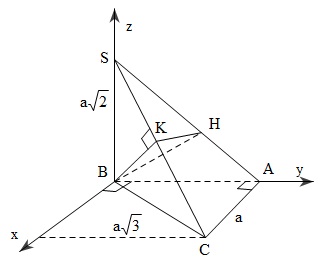
Đề bài: Cho tứ diện $SABC, \Delta ABC$ vuông tại $A$ có $AC=a, BC=a\sqrt{3}, SB=a\sqrt{2}, SB\bot (ABC)  $. Qua $B$ vẽ $BH\bot SA, BK\bot SC (H\in SA, K\in SC)$ a) Chứng minh $SC\bot (BHK)$b) Tính diện tích $\Delta BHK$c) Tính $[A,SC,B]$

Lời giải

Trong $(ABC)$, vẽ $Bx\bot BA$
Ta có: $AB=\sqrt{BC^2-AC^2} =a\sqrt{2} $
$\Rightarrow  \Delta BAS$ vuông cân tại $B$
$\Rightarrow  H$ là trung điểm $SA$
chọn hệ trục tọa độ $Bxyz$ sao cho $B(0;0;0), A(0;a\sqrt{2};0 ), S(0;0;a\sqrt{2} )$
$\Rightarrow  C(a;a\sqrt{0} ), H(0;\frac{a\sqrt{2} }{2};\frac{a\sqrt{2} }{2}  )$

a) Ta có: $\overrightarrow{SC}=(a;a\sqrt{2};-a\sqrt{2}  )=a(1;\sqrt{2};-\sqrt{2}  ) $
$\Rightarrow  $ phương trình tham số $SC: \left\{ \begin{array}{l} x=t\\ y=\sqrt{2}t \\z=a\sqrt{2}-\sqrt{2} t  \end{array} \right. (t\in R)$
$\Rightarrow  K(t;\sqrt{2}t;a\sqrt{2} t )\in SC$
$BK\bot SC\Leftrightarrow  \overrightarrow{BK}.\overrightarrow{SC}=0\Leftrightarrow  (t;\sqrt{2}t;a\sqrt{2}-\sqrt{2}t   )(1;\sqrt{2};-\sqrt{2}  )  =0$
$\Leftrightarrow  t=\frac{2a}{5} \Rightarrow  K(\frac{2a}{5};\frac{2\sqrt{2} a}{5};\frac{3a\sqrt{2} }{5}   )$
$\overrightarrow{BH}.\overrightarrow{SC} =(0;\frac{a\sqrt{2} }{2};\frac{a\sqrt{2} }{2}  )(1;\sqrt{2};-\sqrt{2}  )=0\Rightarrow  BH\bot SC $
Vậy $SC\bot (BHK)$

b)
${S_{\Delta BHK}} = \frac{1}{2}|{\rm{[}}\overrightarrow {BH} {\rm{,}}\overrightarrow {BK} {\rm{]}}| = \frac{1}{2}\left| {\left[ {\left( {0;\frac{{a\sqrt 2 }}{2};\frac{{a\sqrt 2 }}{2}} \right),\left( {\frac{{2a}}{5};\frac{{2\sqrt 2 a}}{5};\frac{{3a\sqrt 2 }}{5}} \right)} \right]} \right| = \frac{{{a^2}\sqrt {13} }}{{10}}$

c) Ta có $SC\bot (BHK)$
$\Rightarrow  \left\{ \begin{array}{l} SC\bot HK\\ SC\bot KB \end{array} \right. \Rightarrow  [A,SC,B]=\widehat{BKH}=(\overrightarrow{KB},\overrightarrow{KH}  )$
$cos(\overrightarrow{KB},\overrightarrow{KH}  )=\frac{\overrightarrow{KB}.\overrightarrow{KH}  }{KB.KH} $
$\begin{array}{l}
                                                    = \frac{{\left( { – \frac{{2a}}{5};\frac{{ – 2a\sqrt 2 }}{5};\frac{{ – 3a\sqrt 2 }}{5}} \right)\left( { – \frac{{2a}}{5};\frac{{a\sqrt 2 }}{{10}};\frac{{ – a\sqrt 2 }}{{10}}} \right)}}{{{a^2}\sqrt {\frac{4}{{25}} + \frac{8}{{25}} + \frac{{18}}{{25}}} \sqrt {\frac{4}{{25}} + \frac{2}{{100}} + \frac{2}{{100}}} }} = \frac{3}{{5\sqrt 6 }}\\
 \Rightarrow c{\rm{os}}[A,SC,B{\rm{] = }}\frac{3}{{5\sqrt 6 }}
\end{array}$