Cho \(f\left( x \right)\)có \(f\left( 0 \right) = 1\)và \(f\left( {\frac{\pi }{4}} \right) = \frac{\pi }{8}\) và \(f'\left( x \right) = \frac{{4m}}{\pi } + {\sin ^2}x\) (với \(m\) là tham số ). Tính \(\int\limits_0^\pi {f\left( x \right)} {\rm{dx}}\) ? A. \( - \frac{\pi }{2} + \frac{{{\pi ^2}}}{8}\). B. \( - 3 + \frac{\pi }{2}\). C. … [Đọc thêm...] vềCho \(f\left( x \right)\)có \(f\left( 0 \right) = 1\)và \(f\left( {\frac{\pi }{4}} \right) = \frac{\pi }{8}\) và \(f’\left( x \right) = \frac{{4m}}{\pi } + {\sin ^2}x\) (với \(m\) là tham số ). Tính \(\int\limits_0^\pi {f\left( x \right)} {\rm{dx}}\) ?
Trắc nghiệm Tích phân
69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là
Câu hỏi: 69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là A. \(\frac{\pi }{2}\left( {{e^2} - 1} \right)\). B. \(\pi \left( {{e^2} + 1} \right)\). C. \(\frac{\pi }{2}\left( {{e^2} + 1} … [Đọc thêm...] về69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là
92. Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = \frac{{x{{\rm{e}}^x}}}{{{{\left( {x + 1} \right)}^2}}}\) và \(F\left( 1 \right) = 1\). Hệ số tự do của \(F\left( x \right)\) thuộc khoảng
Câu hỏi: 92. Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = \frac{{x{{\rm{e}}^x}}}{{{{\left( {x + 1} \right)}^2}}}\) và \(F\left( 1 \right) = 1\). Hệ số tự do của \(F\left( x \right)\) thuộc khoảng A. \(\left( { - \frac{1}{2};\,0} \right)\). B. \(\left( {0;\,\frac{1}{2}} \right)\). C. \(\left( {\frac{1}{2};\,1} \right)\). D. \(\left( { - 1;\, - … [Đọc thêm...] về92. Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = \frac{{x{{\rm{e}}^x}}}{{{{\left( {x + 1} \right)}^2}}}\) và \(F\left( 1 \right) = 1\). Hệ số tự do của \(F\left( x \right)\) thuộc khoảng
4. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x – 3}}{{{x^2} – 3x + 9}}\)là
Câu hỏi: 4. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x - 3}}{{{x^2} - 3x + 9}}\)là A. \(\ln \left| {{x^2} - 3x + 9} \right| + C\). B. \(\frac{1}{{{x^2} - 3x + 9}} + C\). C. \( - \ln \left( {{x^2} - 2x + 9} \right) + C\). D. \(\ln \left( {{x^2} - 2x + 9} \right)\). Lời giải Xét \(\int {f\left( x \right){\rm{d}}x} = \int {\frac{{2x - … [Đọc thêm...] về4. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x – 3}}{{{x^2} – 3x + 9}}\)là
98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) như hình bên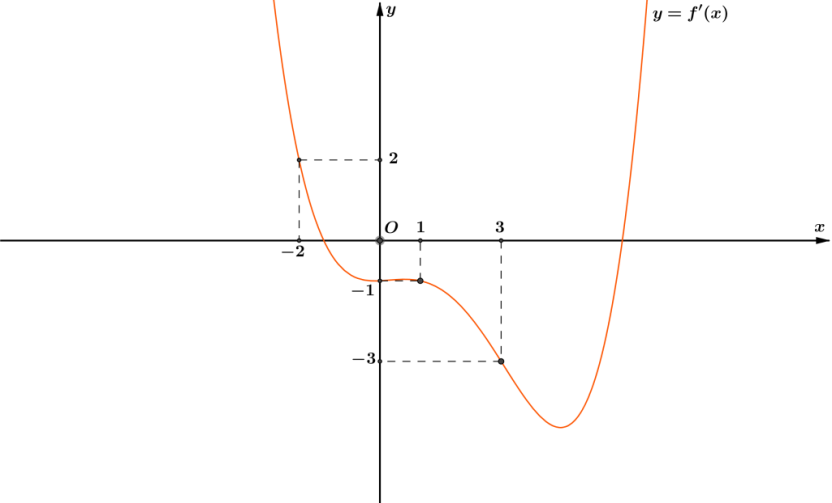
Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng?
Câu hỏi: 98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng? A. \(g\left( 1 \right) < g\left( { - 2} \right) < g\left( 3 \right)\). B. \(g\left( { - 2} \right) > g\left( 3 \right) = … [Đọc thêm...] về98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) như hình bên
Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng?
59. Xét \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \), nếu đặt \(u = \ln x\) thì \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \) bằng
Câu hỏi: 59. Xét \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \), nếu đặt \(u = \ln x\) thì \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \) bằng A. \(\int\limits_0^1 {u{\rm{d}}u} \). B. \(\int\limits_1^e {u{\rm{d}}u} \). C. \(\frac{1}{2}\int\limits_0^1 {u{\rm{d}}u} \). D. \(\int\limits_0^1 {\frac{u}{{{e^u}}}{\rm{d}}u} \). Lời giải Đặt \(u = … [Đọc thêm...] về59. Xét \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \), nếu đặt \(u = \ln x\) thì \(I = \int\limits_1^e {\frac{{\ln x}}{x}{\rm{d}}x} \) bằng
34. Tính nguyên hàm \(\int {\frac{{x – 1}}{{{{\left( {{x^2} – 2x + 3} \right)}^{2021}}}}} {\rm{d}}x\).
Câu hỏi: 34. Tính nguyên hàm \(\int {\frac{{x - 1}}{{{{\left( {{x^2} - 2x + 3} \right)}^{2021}}}}} {\rm{d}}x\). A. \(\frac{{ - 1}}{{2020{{\left( {{x^2} - 2x + 3} \right)}^{2020}}}} + C\). B. \(\frac{{ - 1}}{{4044{{\left( {{x^2} - 2x + 3} \right)}^{2022}}}} + C\). C. \(\frac{{ - 1}}{{4040{{\left( {{x^2} - 2x + 3} \right)}^{2020}}}} + C\). D. … [Đọc thêm...] về34. Tính nguyên hàm \(\int {\frac{{x – 1}}{{{{\left( {{x^2} – 2x + 3} \right)}^{2021}}}}} {\rm{d}}x\).
36. Tính \(\int {\frac{{{{\cos }^3}x}}{{{{\sin }^2}x}}{\rm{d}}x} \) ta được kết quả nào sau đây?
Câu hỏi: 36. Tính \(\int {\frac{{{{\cos }^3}x}}{{{{\sin }^2}x}}{\rm{d}}x} \) ta được kết quả nào sau đây? A. \(\int {\frac{{{{\cos }^3}x}}{{{{\sin }^2}x}}{\rm{d}}x = - \frac{1}{{\sin x}}} + \sin x + C\). B. \(\int {\frac{{{{\cos }^3}x}}{{{{\sin }^2}x}}{\rm{d}}x = - \frac{1}{{\sin x}}} + \cos x + C\). C. \(\int {\frac{{{{\cos }^3}x}}{{{{\sin … [Đọc thêm...] về36. Tính \(\int {\frac{{{{\cos }^3}x}}{{{{\sin }^2}x}}{\rm{d}}x} \) ta được kết quả nào sau đây?
38. Tính \(\int {\frac{{{{\ln }^2}x}}{{x\log x}}} {\rm{d}}x\) ta được kết quả nào sau đây?
Câu hỏi: 38. Tính \(\int {\frac{{{{\ln }^2}x}}{{x\log x}}} {\rm{d}}x\) ta được kết quả nào sau đây? A. \(\frac{{{{\ln }^2}x}}{2} + C\). B. \(\frac{{{{\ln }^2}x}}{{\ln 10}} + C\). C. \(\ln 10.{\ln ^2}x + C\). D. \(\ln 10.\frac{{{{\ln }^2}x}}{2} + C\). Lời giải Ta có \(\int {\frac{{{\rm{l}}{{\rm{n}}^2}x}}{{x.\log x}}} {\rm{dx}}\,{\rm{ = }}\int {\frac{{{{\ln … [Đọc thêm...] về38. Tính \(\int {\frac{{{{\ln }^2}x}}{{x\log x}}} {\rm{d}}x\) ta được kết quả nào sau đây?
53. Hàm số nào sau đây là một nguyên hàm của hàm số \(f(x) = \cos x\sqrt {\sin x + 1} \)?
Câu hỏi: 53. Hàm số nào sau đây là một nguyên hàm của hàm số \(f(x) = \cos x\sqrt {\sin x + 1} \)? A. \(F(x) = \frac{{1 - 2\sin x - 3{{\sin }^2}x}}{{2\sqrt {\sin x + 1} }}\). B. \(F(x) = \frac{2}{3}\left( {\sin x + 1} \right)\sqrt {\sin x + 1} \). C. \(F(x) = \frac{1}{3}\left( {\sin x + 1} \right)\sqrt {\sin x + 1} \). D. \(F(x) = \frac{1}{3}\sin x\sqrt {\sin x … [Đọc thêm...] về53. Hàm số nào sau đây là một nguyên hàm của hàm số \(f(x) = \cos x\sqrt {\sin x + 1} \)?
