Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Cho hàm số:  $y = \frac{x – 2}{x + 1}$.1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số.2)    $M$ là một điểm có hoành đố $a \ne  – 1$, và thuộc đồ thị. Viết phương trình tiếp tuyến của đồ thị tại điểm $M$.3)    Tính khoảng cách từ điểm $I(-1; 1)$ đến tiếp tuyến đó. Xác định $a$ để khoảng cách ấy là lớn nhất

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = \frac{x - 2}{x + 1}$.1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số.2)    $M$ là một điểm có hoành đố $a \ne  - 1$, và thuộc đồ thị. Viết phương trình tiếp tuyến của đồ thị tại điểm $M$.3)    Tính khoảng cách từ điểm $I(-1; 1)$ đến tiếp tuyến đó. Xác định $a$ để khoảng cách ấy là lớn nhất Lời giải $1)$    Dành cho bạn đọc.$2)$    Điểm $M$ thuộc … [Đọc thêm...] vềĐề: Cho hàm số:  $y = \frac{x – 2}{x + 1}$.1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số.2)    $M$ là một điểm có hoành đố $a \ne  – 1$, và thuộc đồ thị. Viết phương trình tiếp tuyến của đồ thị tại điểm $M$.3)    Tính khoảng cách từ điểm $I(-1; 1)$ đến tiếp tuyến đó. Xác định $a$ để khoảng cách ấy là lớn nhất

Đề:  Tìm miền xác định và miền giá trị của các hàm số sau, suy ra giá trị lớn nhất và nhỏ nhất  của các hàm số:$    a) y = \frac{{{cosx – sinx + 1}}}{{{sinx + 2cosx – 42}}}$         $b) y = \frac{{{3sinx}}}{{{2 + cosx}}}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Tìm miền xác định và miền giá trị của các hàm số sau, suy ra giá trị lớn nhất và nhỏ nhất  của các hàm số:$    a) y = \frac{{{cosx - sinx + 1}}}{{{sinx + 2cosx - 42}}}$         $b) y = \frac{{{3sinx}}}{{{2 + cosx}}}$ Lời giải $a)$ Ta có : $sinx +2cosx-42\leq -39$ Do $-1\leq sinx\leq 1$ và $-1\leq cosx\leq 1$TXĐ: $D = R$Gọi $y_0$ là một giá trị của hàm … [Đọc thêm...] vềĐề:  Tìm miền xác định và miền giá trị của các hàm số sau, suy ra giá trị lớn nhất và nhỏ nhất  của các hàm số:$    a) y = \frac{{{cosx – sinx + 1}}}{{{sinx + 2cosx – 42}}}$         $b) y = \frac{{{3sinx}}}{{{2 + cosx}}}$

Đề:   Cho hàm số: $f(x) = {x^3} -ax $$a)$ Khảo sát và vẽ đồ thị hàm số với $a = 3$. Gọi đồ thị này là ($G$). Viết phương trình của Parabol đi qua các điểm $A( – \sqrt 3 ;0)\,\,\,B(\sqrt 3 ;0)$ và tiếp xúc với ($G$)$b)$ Với những giá trị nào của $x$ thì tồn tại $t \ne x$ sao cho $f(x) = f(t).$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:   Cho hàm số: $f(x) = {x^3} -ax $$a)$ Khảo sát và vẽ đồ thị hàm số với $a = 3$. Gọi đồ thị này là ($G$). Viết phương trình của Parabol đi qua các điểm $A( - \sqrt 3 ;0)\,\,\,B(\sqrt 3 ;0)$ và tiếp xúc với ($G$)$b)$ Với những giá trị nào của $x$ thì tồn tại $t \ne x$ sao cho $f(x) = f(t).$ Lời giải $a.$  Với $a=3,f(x)=x^3-3x.$ Khảo sát và vẽ đồ thịXin dành cho bạn … [Đọc thêm...] vềĐề:   Cho hàm số: $f(x) = {x^3} -ax $$a)$ Khảo sát và vẽ đồ thị hàm số với $a = 3$. Gọi đồ thị này là ($G$). Viết phương trình của Parabol đi qua các điểm $A( – \sqrt 3 ;0)\,\,\,B(\sqrt 3 ;0)$ và tiếp xúc với ($G$)$b)$ Với những giá trị nào của $x$ thì tồn tại $t \ne x$ sao cho $f(x) = f(t).$

Đề: Cho hàm số \(y = 2x – 1 + \frac{{2m}}{{x – 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số \(y = 2x - 1 + \frac{{2m}}{{x - 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi. Lời giải $1$. Bạn đọc tự giải.$2$.  Hàm số có cực đại và cực tiểu \( \Leftrightarrow y' = \frac{{2{x^2} - 4x + 2 … [Đọc thêm...] vềĐề: Cho hàm số \(y = 2x – 1 + \frac{{2m}}{{x – 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi.

Đề: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = \begin{cases}x^2 \cos \frac{1}{x}  khi  x \neq  0  \\ 0   khi  x = 0\end{cases}$tại điểm $x_0 = 0$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = \begin{cases}x^2 \cos \frac{1}{x}  khi  x \neq  0  \\ 0   khi  x = 0\end{cases}$tại điểm $x_0 = 0$ Lời giải Hàm số $f(x)$ xác định trong một lân cận của $x_0=0$.Ta có :       $ f'(0) = \mathop {\lim }\limits_{x \to 0} \frac{f(x) - f(0)}{x-0} = \mathop {\lim }\limits_{x \to 0} x.\cos \frac{1}{x}$.Ta có :* Với mọi $x … [Đọc thêm...] vềĐề: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = \begin{cases}x^2 \cos \frac{1}{x}  khi  x \neq  0  \\ 0   khi  x = 0\end{cases}$tại điểm $x_0 = 0$

Đề: Xác định tính chẵn, lẻ của các hàm số sau:a)    \(y=|x+2|-|x-2|\)b)    \(y=|2x+1|+|2x-1|\)

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Xác định tính chẵn, lẻ của các hàm số sau:a)    \(y=|x+2|-|x-2|\)b)    \(y=|2x+1|+|2x-1|\) Lời giải a)    \(y=f(x)=|x+2|-|x-2|\) có tập xác định là \(R\) đối xứng.Ta có: \(f(-x)=|-x+2|-|-x-2|\\\Leftrightarrow f(-x)=-f(x)\).Vậy: \(f(x)=|x+2|-|x-2|\) là hàm số lẻb)    \(f(x)=|2x+1|+|2x-1|\) có tập xác định là \(R\) đối xứng.Ta … [Đọc thêm...] vềĐề: Xác định tính chẵn, lẻ của các hàm số sau:a)    \(y=|x+2|-|x-2|\)b)    \(y=|2x+1|+|2x-1|\)

Đề: Tìm giá trị lớn nhất của biểu thức hàm số $f(x)=|\sqrt{x^2-2x+5}-\sqrt{x^2-12x+136}|$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị lớn nhất của biểu thức hàm số $f(x)=|\sqrt{x^2-2x+5}-\sqrt{x^2-12x+136}|$ Lời giải Để ý $\begin{cases}x^2-2x+5=(x-1)^2+4 \geq 4, \forall x \in R \\ x^2-12x+136=(6-x)^2+100, \forall x \in R \end{cases}$do vậy hàm số xác định  với $\forall x \in R$* Xét các vectơ : $\overrightarrow a=(x-1;-2), \overrightarrow b(6-x;10)$. Ta có $|\overrightarrow … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất của biểu thức hàm số $f(x)=|\sqrt{x^2-2x+5}-\sqrt{x^2-12x+136}|$

Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x – \frac{1}{{x + 1}}$$2$. Chứng tỏ rằng đồ thị này nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.$3$. Tìm tất cả các cặp điểm trên đồ thị của hàm số mà các tiếp tuyến tại đó song song với nhau.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x - \frac{1}{{x + 1}}$$2$. Chứng tỏ rằng đồ thị này nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.$3$. Tìm tất cả các cặp điểm trên đồ thị của hàm số mà các tiếp tuyến tại đó song song với nhau. Lời giải $1.$ Xin dành cho bạn đọc. .$2.$ Gọi $G$ là giao diểm $2$ tiệm cận thì $G(-1,-1)$.  Đặt … [Đọc thêm...] vềĐề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x – \frac{1}{{x + 1}}$$2$. Chứng tỏ rằng đồ thị này nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.$3$. Tìm tất cả các cặp điểm trên đồ thị của hàm số mà các tiếp tuyến tại đó song song với nhau.

Đề: Dùng định nghĩa để tìm khoảng tăng giảm của hàm số:                      \(f(x)=-x^{2}+4x-1\) 

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Dùng định nghĩa để tìm khoảng tăng giảm của hàm số:                      \(f(x)=-x^{2}+4x-1\)  Lời giải Miền xác định:\(D=R\)\(\forall x_{1},x_{2} \in R\) và \(x_{1}\leq x_{2}\). Ta có:\(f(x_{1})-f(x_{2})=(-x_{1}^{2}+4x_{1}-1)-(-x_{2}^{2}+4x_{2}-1)\)                            \(=(x_{2}^{2}-x_{1}^{2})+4(x_{1}-x_{2})=(x_{2}-x_{1})(x_{1}+x_{2}-4)\)_Vì \(x_{1}\leq … [Đọc thêm...] vềĐề: Dùng định nghĩa để tìm khoảng tăng giảm của hàm số:                      \(f(x)=-x^{2}+4x-1\) 

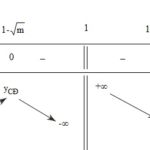
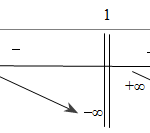
Đề: Biện luận theo $m$ số nghiệm của phương trình:  $\frac{x}{\ln x}=\ln m$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Biện luận theo $m$ số nghiệm của phương trình:  $\frac{x}{\ln x}=\ln m$ Lời giải Trước hết với $m\leq 0$ phương trình vô nghiệm, xét với $m>0$.Số nghiệm của phương trình là số giao điểm của đường thẳng $y=\ln m$ với đồ thị hàm số $y=\frac{x}{\ln x}$.  Xét hàm sô $y=\frac{x}{\ln x}$ .-Miền xác định $D=(0; +\infty) \setminus \left\{ {1} \right\}$.-Đạo hàm … [Đọc thêm...] vềĐề: Biện luận theo $m$ số nghiệm của phương trình:  $\frac{x}{\ln x}=\ln m$