Khảo sát và vẽ đồ thị hàm số

Đề: Cho phương trình: $2\cos x\cos2x\cos3x+m=7\cos2x$a) Giải phương trình với $m = – 7$b) xác định $m$ để phương trình có nhiều hơn một nghiệm x thuộc đoạn $[ { – \frac{{3\pi }}{8}; – \frac{\pi }{8}} ]$

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

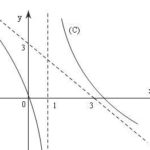
Đề bài: Cho phương trình: $2\cos x\cos2x\cos3x+m=7\cos2x$a) Giải phương trình với $m = - 7$b) xác định $m$ để phương trình có nhiều hơn một nghiệm x thuộc đoạn $[ { - \frac{{3\pi }}{8}; - \frac{\pi }{8}} ]$ Lời giải Ta có: $2\cos {\rm{x}}c{\rm{os}}3{\rm{x}} = c{\rm{os4x}} + c{\rm{os}}2{\rm{x}} = 2c{\rm{o}}{{\rm{s}}^2}2{\rm{x}} - 1 + c{\rm{os2x}}$ Do đó phương … [Đọc thêm...] vềĐề: Cho phương trình: $2\cos x\cos2x\cos3x+m=7\cos2x$a) Giải phương trình với $m = – 7$b) xác định $m$ để phương trình có nhiều hơn một nghiệm x thuộc đoạn $[ { – \frac{{3\pi }}{8}; – \frac{\pi }{8}} ]$

Đề: Cho hàm số $y=\frac{(m+1)x+m}{x+m} $a) Với $m = 1$:i) Khảo sát sự biến thiên và vẽ đồ thị hàm số.ii) Tìm trên đồ thị những điểm có tổng khoảng cách đến hai tiệm cận là nhỏ nhất.b) Chứng minh rằng với mọi $m \ne 0$, đồ thị của hàm số luôn tiếp xúc một đường thẳng cố định

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số $y=\frac{(m+1)x+m}{x+m} $a) Với $m = 1$:i) Khảo sát sự biến thiên và vẽ đồ thị hàm số.ii) Tìm trên đồ thị những điểm có tổng khoảng cách đến hai tiệm cận là nhỏ nhất.b) Chứng minh rằng với mọi $m \ne 0$, đồ thị của hàm số luôn tiếp xúc một đường thẳng cố định Lời giải a) Với $m = 1$:$y = \frac{{2x + 1}}{{x + 1}} = 2 - \frac{1}{{x + 1}}$i) Dành … [Đọc thêm...] vềĐề: Cho hàm số $y=\frac{(m+1)x+m}{x+m} $a) Với $m = 1$:i) Khảo sát sự biến thiên và vẽ đồ thị hàm số.ii) Tìm trên đồ thị những điểm có tổng khoảng cách đến hai tiệm cận là nhỏ nhất.b) Chứng minh rằng với mọi $m \ne 0$, đồ thị của hàm số luôn tiếp xúc một đường thẳng cố định

Đề: Cho hàm số $y = {x^3} + 3{x^2} + mx + m$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số với $m = 0$$2$. Tìm tất cả các giá trị của tham số $m$ để hàm số nghịch biến trên một đoạn có độ dài bằng $1$.

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số $y = {x^3} + 3{x^2} + mx + m$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số với $m = 0$$2$. Tìm tất cả các giá trị của tham số $m$ để hàm số nghịch biến trên một đoạn có độ dài bằng $1$. Lời giải $1$. Bạn đọc tự giải.$2$. $f\left( x \right) = {x^3} - 3{x^2} + mx + m $$f'\left( x \right) = 3{x^2} + 6x + m \Rightarrow f'\left( x \right)$ có … [Đọc thêm...] vềĐề: Cho hàm số $y = {x^3} + 3{x^2} + mx + m$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số với $m = 0$$2$. Tìm tất cả các giá trị của tham số $m$ để hàm số nghịch biến trên một đoạn có độ dài bằng $1$.

Đề: Cho hàm số: $y = 4x^3 – mx^2 – 3x + m$$1.$ Chứng minh rằng với mọi m hàm số luôn luôn có cực đại và cực tiểu, đồng thời chứng minh rằng hoành độ cực đại và hoành độ cực tiểu của hàm số luôn luôn trái dấu.$2.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $m = 0$$3.$ Phương trình $4{x^3} – 3x = \sqrt {1 – x^2} $ có bao nhiêu nghiệm?

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = 4x^3 - mx^2 - 3x + m$$1.$ Chứng minh rằng với mọi m hàm số luôn luôn có cực đại và cực tiểu, đồng thời chứng minh rằng hoành độ cực đại và hoành độ cực tiểu của hàm số luôn luôn trái dấu.$2.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $m = 0$$3.$ Phương trình $4{x^3} - 3x = \sqrt {1 - x^2} $ có bao nhiêu nghiệm? Lời giải $1.$ $y' = … [Đọc thêm...] vềĐề: Cho hàm số: $y = 4x^3 – mx^2 – 3x + m$$1.$ Chứng minh rằng với mọi m hàm số luôn luôn có cực đại và cực tiểu, đồng thời chứng minh rằng hoành độ cực đại và hoành độ cực tiểu của hàm số luôn luôn trái dấu.$2.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $m = 0$$3.$ Phương trình $4{x^3} – 3x = \sqrt {1 – x^2} $ có bao nhiêu nghiệm?

Đề: Cho hàm số: $y = – x + 3 + \frac{3}{x – 1}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số. Từ đó suy ra đồ thị của hàm số: $y = \frac{{ – {x^2} + 4x}}{{|x – 1|}}$$2.$ Chứng minh rằng đường thẳng $y = 2x + m$ luôn luôn cắt $(Cm)$ tại hai điểm phân biệt có hoành độ $x_1; x_2$. Tìm các giá trị của $m$ sao cho $d = {({x_1} – {x_2})^2}$ đạt giá trị bé nhất.

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = - x + 3 + \frac{3}{x - 1}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số. Từ đó suy ra đồ thị của hàm số: $y = \frac{{ - {x^2} + 4x}}{{|x - 1|}}$$2.$ Chứng minh rằng đường thẳng $y = 2x + m$ luôn luôn cắt $(Cm)$ tại hai điểm phân biệt có hoành độ $x_1; x_2$. Tìm các giá trị của $m$ sao cho $d = {({x_1} - … [Đọc thêm...] vềĐề: Cho hàm số: $y = – x + 3 + \frac{3}{x – 1}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số. Từ đó suy ra đồ thị của hàm số: $y = \frac{{ – {x^2} + 4x}}{{|x – 1|}}$$2.$ Chứng minh rằng đường thẳng $y = 2x + m$ luôn luôn cắt $(Cm)$ tại hai điểm phân biệt có hoành độ $x_1; x_2$. Tìm các giá trị của $m$ sao cho $d = {({x_1} – {x_2})^2}$ đạt giá trị bé nhất.

Đề: Cho hàm số: $y = {x^4} – a{x}^3 – (2a + 1){x^2} + ax + 1$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = 0$.2) Tìm điểm $A$ thuộc trục tung sao cho qua $A$ có thể kẻ được ba tiếp tuyến với đồ thị ở phần 1

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = {x^4} - a{x}^3 - (2a + 1){x^2} + ax + 1$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = 0$.2) Tìm điểm $A$ thuộc trục tung sao cho qua $A$ có thể kẻ được ba tiếp tuyến với đồ thị ở phần 1 Lời giải $1)$ Dành cho bạn đọc.$2)$ Điểm A có tọa độ $(0,{\rm{ }}{{\rm{y}}_o})$ và phương trình tiếp tuyến qua A có dạng $y = kx + {y_o}$. Hoành độ tiếp … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^4} – a{x}^3 – (2a + 1){x^2} + ax + 1$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $a = 0$.2) Tìm điểm $A$ thuộc trục tung sao cho qua $A$ có thể kẻ được ba tiếp tuyến với đồ thị ở phần 1

Đề: Cho hàm số $y = \frac{{2{x^2} – 3x + m}}{{x – 1}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$$2$. Biện luận theo tham số $a$ về số nghiệm của phương trình $\frac{{2{x^2} – 3x + 2}}{{x – 1}} + {\log _{\frac{1}{2}}}a = 0$$3$. Với những giá trị nào của $m$ thì hàm số đã cho là đồng biến trên khoảng $\left( {3; + \infty } \right)$

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số $y = \frac{{2{x^2} - 3x + m}}{{x - 1}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$$2$. Biện luận theo tham số $a$ về số nghiệm của phương trình $\frac{{2{x^2} - 3x + 2}}{{x - 1}} + {\log _{\frac{1}{2}}}a = 0$$3$. Với những giá trị nào của $m$ thì hàm số đã cho là đồng biến trên khoảng $\left( {3; + \infty } \right)$ Lời giải $1$. Bạn … [Đọc thêm...] vềĐề: Cho hàm số $y = \frac{{2{x^2} – 3x + m}}{{x – 1}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$$2$. Biện luận theo tham số $a$ về số nghiệm của phương trình $\frac{{2{x^2} – 3x + 2}}{{x – 1}} + {\log _{\frac{1}{2}}}a = 0$$3$. Với những giá trị nào của $m$ thì hàm số đã cho là đồng biến trên khoảng $\left( {3; + \infty } \right)$

Đề: Cho hàm số $y$ = $\frac{{\left( {m + 1} \right){x^2} – 2mx – \left( {{m^3} – {m^2} + 2} \right)}}{{x – m}}\left( {{C_m}} \right)$$1$. Khảo sát hàm số với $m = 0$$2$. Xác định tất cả các giá trị của $m$ sao cho hàm số luôn luôn nghịch biến trên các khoảng xác định của nó.

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số $y$ = $\frac{{\left( {m + 1} \right){x^2} - 2mx - \left( {{m^3} - {m^2} + 2} \right)}}{{x - m}}\left( {{C_m}} \right)$$1$. Khảo sát hàm số với $m = 0$$2$. Xác định tất cả các giá trị của $m$ sao cho hàm số luôn luôn nghịch biến trên các khoảng xác định của nó. Lời giải $1$. Bạn đọc tự giải$2$. Ta có $y' = \frac{{\left( {m + 1} \right){x^2} - 2m\left( … [Đọc thêm...] vềĐề: Cho hàm số $y$ = \(\frac{{\left( {m + 1} \right){x^2} – 2mx – \left( {{m^3} – {m^2} + 2} \right)}}{{x – m}}\left( {{C_m}} \right)$$1$. Khảo sát hàm số với $m = 0$$2$. Xác định tất cả các giá trị của $m$ sao cho hàm số luôn luôn nghịch biến trên các khoảng xác định của nó.

Đề: Cho hàm số: $y = f(x) = \frac{mx^2 + (m – 1)x + {m^2} + m}{{x – m}}\,\,\,\,\,(1)$$a$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1$.Từ đồ thị vẽ suy ra đồ thị:$y = \frac{{{x^2} + 2}}{{|x| – 1}}$$ b)$ Tìm $x_0$ để với mọi $m \ne 0$, tiếp tuyến của đồ thị ($1$) tại điểm có hoành độ $x_0$ song song với một đường thẳng cố định. Tìm hệ số góc của đường thẳng cố định ấy.

Ngày 15/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = f(x) = \frac{mx^2 + (m - 1)x + {m^2} + m}{{x - m}}\,\,\,\,\,(1)$$a$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1$.Từ đồ thị vẽ suy ra đồ thị:$y = \frac{{{x^2} + 2}}{{|x| - 1}}$$ b)$ Tìm $x_0$ để với mọi $m \ne 0$, tiếp tuyến của đồ thị ($1$) tại điểm có hoành độ $x_0$ song song với một đường thẳng cố định. Tìm hệ số góc của đường … [Đọc thêm...] vềĐề: Cho hàm số: $y = f(x) = \frac{mx^2 + (m – 1)x + {m^2} + m}{{x – m}}\,\,\,\,\,(1)$$a$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1$.Từ đồ thị vẽ suy ra đồ thị:$y = \frac{{{x^2} + 2}}{{|x| – 1}}$$ b)$ Tìm $x_0$ để với mọi $m \ne 0$, tiếp tuyến của đồ thị ($1$) tại điểm có hoành độ $x_0$ song song với một đường thẳng cố định. Tìm hệ số góc của đường thẳng cố định ấy.

Đề: Cho hàm số: $y = \frac{2x + 1}{x + 2} (H)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($H$) của hàm số. Tính diện tích hình phẳng giới hạn bởi ($H$) , trục hoành và đường thẳng $x = 1$$2$. Tìm những giá trị của $t$ để phương trình $\frac{2\sin x + 1}{\sin x + 2} = t$ có đúng hai nghiệm thuộc khoảng $[0;\pi $].

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = \frac{2x + 1}{x + 2} (H)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($H$) của hàm số. Tính diện tích hình phẳng giới hạn bởi ($H$) , trục hoành và đường thẳng $x = 1$$2$. Tìm những giá trị của $t$ để phương trình $\frac{2\sin x + 1}{\sin x + 2} = t$ có đúng hai nghiệm thuộc khoảng $[0;\pi $]. Lời giải $1.$ Bạn đọc tự giải$2.$ Đặt … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{2x + 1}{x + 2} (H)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($H$) của hàm số. Tính diện tích hình phẳng giới hạn bởi ($H$) , trục hoành và đường thẳng $x = 1$$2$. Tìm những giá trị của $t$ để phương trình $\frac{2\sin x + 1}{\sin x + 2} = t$ có đúng hai nghiệm thuộc khoảng $[0;\pi $].